A numerical solver based on two-dimensional Poisson and drift-diffusion
equations with Gaussian-shaped density of states, the Poole--Frenkel
field mobility model, and the Ising model is proposed to analyze carrier
transport in the host--guest systems based on organic semiconductors.
To investigate the performance of this solver, a series of the electron-
only devices and hole-only devices are fabricated with different dopant
concentrations. The space-charge-limited current model is applied to the
simulation results to calculate the mobility. In addition, experimental
results for different host--guest systems are compared to prove the
accuracy of the solver. The solver is able to explain the physical
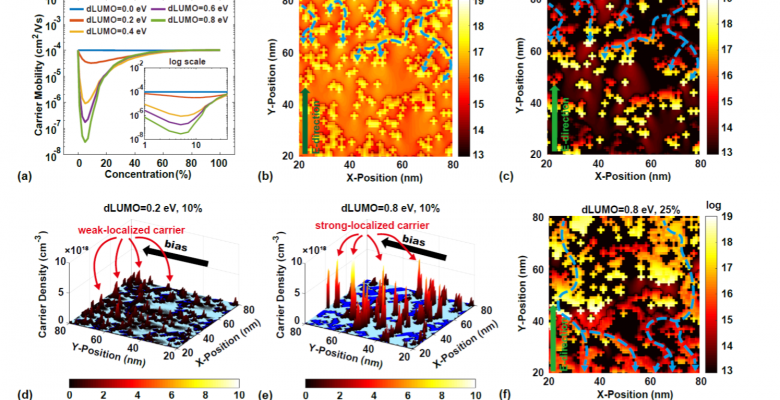
mechanisms in different situations. At lower dopant concentrations, the
guest states act as traps. Carriers are localized in these guest states,
and the carrier mobility decreases dramatically. At the higher dopant
concentrations, regions of guest material are able to connect with each
other, and carriers have a probability to hop through the guest states.
The mobility characteristics gradually approach those of the pure guest
material.
Jun-Yu Huang, Jiun-Haw Lee, Yuh-Renn Wu, Tse-Ying Chen, Yu-Cheng Chiu, Jau-Jiun Huang, Man-kit Leung, Tien-Lung Chiu
Phys. Rev. Materials 4, 125602 – Published 17 December 2020
https://journals.aps.org/prmaterials/abstract/10.1103/PhysRevMaterials.4.125602