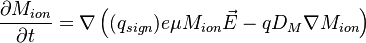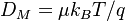"$Withionmove" 修訂間的差異

出自 DDCC TCAD TOOL Manual
前往： 導覽、 搜尋
行 5： 行 5：
 
Ideally, the ion density is given by initial setting. The total ion number should be fixed. The program is aim to model multi-ions drift-diffusion. The command is as following.
 
Ideally, the ion density is given by initial setting. The total ion number should be fixed. The program is aim to model multi-ions drift-diffusion. The command is as following.
 
$Withionmove
  
$Withionmove
−
<math> N_sweep </math> <math> N_output</math>
 +
<math> N_sweep </math> <math> N_{output}</math>
 
<math>T_{1,stop}</math> <math>dt_{1}</math> <math>T_{2,stop}</math> <math>dt_{2}</math> ... <math>T_{N_{sweep},stop}</math> <math>dT_{M_{sweep}}</math>
  
<math>T_{1,stop}</math> <math>dt_{1}</math> <math>T_{2,stop}</math> <math>dt_{2}</math> ... <math>T_{N_{sweep},stop}</math> <math>dT_{M_{sweep}}</math>
 
<math> N_{ions} ~~ q_{sign,1} ~~ q_{sign,2} ~~ q_{sign,3} ....~~ q_{sign,N_{ions}} </math>
  
<math> N_{ions} ~~ q_{sign,1} ~~ q_{sign,2} ~~ q_{sign,3} ....~~ q_{sign,N_{ions}} </math>

於 2019年8月18日 (日) 11:49 的修訂

When the system has ion to perform as drift-diffusion equations, we solve the time dependent drift-diffusion for slow ion move simulation. Since the ion moves may not be governed fermi-level concept. We simply treat is a tradiational drift-diffusion equations. 

 \frac{\partial M_{ion}}{\partial t} = \nabla \left( (q_{sign}) e\mu M_{ion} \vec{E} - q D_{M} \nabla M_{ion} \right)

Ideally, the ion density is given by initial setting. The total ion number should be fixed. The program is aim to model multi-ions drift-diffusion. The command is as following. 

$Withionmove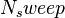
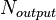
 N_sweep   N_{output}
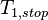
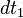
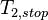
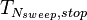
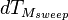
T_{1,stop}  dt_{1} T_{2,stop}  dt_{2} ... T_{N_{sweep},stop}  dT_{M_{sweep}}
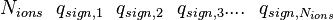
 N_{ions} ~~ q_{sign,1} ~~ q_{sign,2} ~~ q_{sign,3}  ....~~ q_{sign,N_{ions}} 
 P_{type,1} ~~ M_{ions,1} \mu  p3 p4 Parameters of the 1 layer
 P_{type,2} ~~ M_{ions,2} \mu  p3 p4 Parameters of the 2 layer
 P_{type,3} ~~ M_{ions,3} \mu  p3 p4 Parameters of the 3 layer
 ....
 .....
 P_{type,N} ~~ M_{ions,N} \mu  p3 p4 Parameters of the $totalregion layer


For example: Consider 2 ions, 1st is negative charges, 2nd is positive charges, total 5 Regions we can 

$Withionmove
1 1000
1.00  1.0d-4 
2 -1.0 1.0
1 0.0e17 0.0      0.0e17 0.0   
1 1.0e17 1.0e-11  2.0e17 1.0e-12
1 1.0e17 1.0e-11  2.0e17 1.0e-12
1 1.0e17 1.0e-11  2.0e17 1.0e-12
1 1.0e17 1.0e-11  2.0e17 1.0e-12

P_{type,1} is the parameter type:  it depends on ion number  N_{ions}
1:  M_{ions,1} ~~~\mu ,  M_{ions,2} ~~~\mu ,........  M_{ions,N_{ions}}, ~~~\mu_{N_{ions}}
2:  M_{ions,1} ~~~\mu ~ D_{M},  M_{ions,2} ~~~\mu~~D_{M} ,........  M_{ions,N_{ions}}, ~~~\mu_{N_{ions}}~~ D_{M}

When type 1 is chosen, we only put mobility 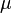\mu , and the diffusion coefficient 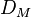D_{M} is calculated with Einstein relation, where 

  D_{M} = \mu k_{B} T / q
取自 "http://yrwu-wk.ee.ntu.edu.tw/mediawiki/index.php?title=$Withionmove&oldid=2006"