"$MaterialParameter" 修訂間的差異
出自 DDCC TCAD TOOL Manual
(→Related commands) |
|||
| 行 1: | 行 1: | ||
=='''Format'''== |
=='''Format'''== |
||
$MaterialParameter |
$MaterialParameter |
||
| − | ''int fp'' <font color=green>// where ''int'' is an integer, and ''fp'' is an floating point.</font> |
||
| + | ''type<sub>dis</sub> N ε<sub>r,∞</sub> μ<sub>r</sub> σ<sub>E</sub> σ<sub>H</sub>'' |
||
| + | ''par<sub>1</sub>(1) par<sub>1</sub>(2) par<sub>1</sub>(3) par<sub>1</sub>(4)'' |
||
| + | ''par<sub>2</sub>(1) par<sub>2</sub>(2) par<sub>2</sub>(3) par<sub>2</sub>(4)'' |
||
| + | . . . . |
||
| + | . . . . |
||
| + | . . . . |
||
| + | ''par<sub>p</sub>(1) par<sub>p</sub>(2) par<sub>p</sub>(3) par<sub>p</sub>(4)'' |
||
| + | . . . . |
||
| + | . . . . |
||
| + | . . . . |
||
| + | ''par<sub>N</sub>(1) par<sub>N</sub>(2) par<sub>N</sub>(3) par<sub>N</sub>(4)'' <font color=green>// where ''type<sub>dis</sub>'' and ''N'' are integers, but the others are floating points.</font> |
||
<font size=3> |
<font size=3> |
||
| − | obj%disper(i),obj%npole(i),obj%eps_inf(i),obj%mur(i),obj%sigE(i),obj%sigH(i) <br> |
||
| + | Refer to Chap. 9 at p.353 - p.368.<br> |
||
| − | pole(i)%par(:,j) where j=1~4 |
||
| + | ''type<sub>dis</sub>'' means the type of dispersive model. ''N'' means the number of poles in this material. ''ε<sub>r,∞</sub>'' is the relative permittivity at infinite frequency, ''μ<sub>r</sub>'' is relative permeability, ''σ<sub>E</sub>'' is electric conductivity, and ''σ<sub>H</sub>'' is equivalent magnetic loss, respectively. |
||
</font> |
</font> |
||
| + | |||
| + | {| class=wikitable style="text-align: center |
||
| + | |+ |
||
| + | |- |
||
| + | || Models || ''type<sub>dis</sub>'' || par<sub>p</sub>(1) || par<sub>p</sub>(2) || par<sub>p</sub>(3) || par<sub>p</sub>(4) |
||
| + | |- |
||
| + | || non-dispersive || 0 || 0 || 0 || 0 || 0 |
||
| + | |- |
||
| + | || Debye || 1 || ε<sub>s,p</sub> || ε<sub>∞,p</sub> || τ<sub>p</sub> || 0 |
||
| + | |- |
||
| + | || Lorentz || 2 || ε<sub>s,p</sub> || ε<sub>∞,p</sub> || ω<sub>p</sub> || δ<sub>p</sub> |
||
| + | |- |
||
| + | || Drude || 3 || ω<sub>i</sub> || γ<sub>p</sub> || 0 || 0 |
||
| + | |} |
||
| + | |||
| + | <math>\varepsilon(\omega) = \varepsilon_\infty + \sum_{p=1}^P \chi_p(\omega)</math><br> |
||
| + | |||
| + | <font size=4>Debye model: </font><math>\chi_p(\omega) = \frac{(\varepsilon_{s,p}-\varepsilon_{\infty,p})}{1+j\omega\tau_p}</math><br><br> |
||
| + | <font size=4>Lorentz model: </font><math>\chi_p(\omega) = \frac{(\varepsilon_{s,p}-\varepsilon_{\infty,p})\omega_p^2}{\omega_p^2+2j\omega\delta_p-\omega^2}</math><br><br> |
||
| + | <font size=4>Drude model: </font><math>\chi_p(\omega) = -\frac{\omega_p^2}{\omega^2-j\omega\gamma_p}</math><br><br> |
||
| + | |||
=='''Example'''== |
=='''Example'''== |
||
| + | $NumberofObject |
||
| + | 1 |
||
$MaterialParameter |
$MaterialParameter |
||
2 3 10 1 0 0 |
2 3 10 1 0 0 |
||
| 行 14: | 行 47: | ||
10 7 2.5133e15 2e14 |
10 7 2.5133e15 2e14 |
||
10 7 3.7699e15 3e14 |
10 7 3.7699e15 3e14 |
||
| − | |||
| − | This means the program has 2 objects in the simulation. |
||
於 2018年7月16日 (一) 13:06 的修訂
Format
$MaterialParameter typedis N εr,∞ μr σE σH par1(1) par1(2) par1(3) par1(4) par2(1) par2(2) par2(3) par2(4) . . . . . . . . . . . . parp(1) parp(2) parp(3) parp(4) . . . . . . . . . . . . parN(1) parN(2) parN(3) parN(4) // where typedis and N are integers, but the others are floating points.
Refer to Chap. 9 at p.353 - p.368.
typedis means the type of dispersive model. N means the number of poles in this material. εr,∞ is the relative permittivity at infinite frequency, μr is relative permeability, σE is electric conductivity, and σH is equivalent magnetic loss, respectively.
| Models | typedis | parp(1) | parp(2) | parp(3) | parp(4) |
| non-dispersive | 0 | 0 | 0 | 0 | 0 |
| Debye | 1 | εs,p | ε∞,p | τp | 0 |
| Lorentz | 2 | εs,p | ε∞,p | ωp | δp |
| Drude | 3 | ωi | γp | 0 | 0 |

Debye model: 
Lorentz model: 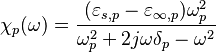
Drude model: 
Example
$NumberofObject 1 $MaterialParameter 2 3 10 1 0 0 10 7 1.2566e15 1e14 10 7 2.5133e15 2e14 10 7 3.7699e15 3e14
Related commands
- Input file 1: $NumberofObject, $MaterialStructure
- Input file 2: $Backgroundparameter