"$callexciton" 修訂間的差異

於 2021年8月17日 (二) 10:52 的修訂

</math>Function for calculate the exciton distribution. We usually use this equation for organic material. Behavior of exciton will follow this equation. You can see the detail in Subroutine_exciton1D.

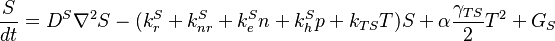
Singlet Rate Equation: $\frac{S}{dt}=D^S{\nabla}^2{S}-(k_{r}^S+k_{nr}^S+k_{e}^Sn+k_{h}^Sp+k_{TS}T)S+\alpha\frac{\gamma_{TS}}{2}{T}^2+G_{S}$

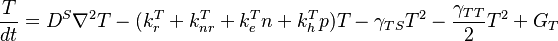
Triplet Rate Equation: $\frac{T}{dt}=D^S{\nabla}^2{T}-(k_{r}^T+k_{nr}^T+k_{e}^Tn+k_{h}^Tp)T-\gamma_{TS}T^2-\frac{\gamma_{TT}}{2}{T}^2+G_{T}$

Physical Mechanics
1. Exciton Diffusion:

$D^S{\nabla}^2{n_{ex}}$

2. Exciton Quenching: $[n^{T,S}_{1}\rightarrow n^{T,S}_{0}]$

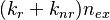
$(k_{r}+k_{nr})n_{ex}$

3. Singlet-Polaron Quenching: $[S_1+n/p\rightarrow S_0+n/p^{*}]$

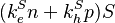
$(k_{e}^Sn+k_{h}^Sp)S$

4. Triplet-Polaron Quenching: $(k_{e}^Tn+k_{h}^Tp)T, [T_1+n/p\rightarrow S_0+n/p^{*}]$

5. Triplet-Singlet Quenching: $k_{TS}TS, [S_1+T_1\rightarrow S_0+T_1]$

6. Triplet-Triplet Annihilation: $\gamma_{TS}T^2+\frac{\gamma_{TT}}{2}{T}^2, [T_1+T_1\rightarrow S_0+T_1] \& [T_1+T_1\rightarrow S_1+S_0]$

7. Triplet-Triplet Fusion: $\alpha\frac{\gamma_{TS}}{2}{T}^2, [T_1+T_1\rightarrow S_1+S_0]$

Where　

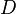$D$ is diffusion coefficient.
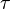$\tau$ is relaxation time of exciton.
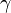$\gamma$ is annihilation rate constant.
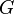$G$ is exciton generation rate.

Format

$callexciton
n
a 4 b c d f
d kr knr gamma g

Parameter Explanation

n : the number of tables we usually set n as 5.
a : The type of exciton solver mode

 1: Time-dependent triplet solver 
 123: Time-dependent triplet and singlet solver (For TADF OLEDs model)
 3: Triplet Exciton Solver (For PhOLEDs model)
 6: Singlet and Triplet Exciton Solver (For TADF OLEDs model)
 4: Triplet Exciton Solver with exciton blocking boundary 
 7: Singlet-Triplet Exciton Solver (For TTF/TADF OLEDs)
 71: Time-dependent singlet-triplet exciton solver with pumping time (For TTF/TADF OLEDs)
 711: Time-dependent singlet-triplet exciton solver (For TTF/TADF's TrEL and TRPL spectrum)

b : Start time (For time-dependent solver)
c : dt (For time-dependent solver)
d : End time (For time-dependent solver)
e : savenum (For time-dependent solver)
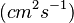
D : diffusion coefficient. $(cm^{2}s^{-1})$
kr : radiatvie rate constant $(s^{-1})$
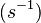
knr :non-radiative rate constant $(s^{-1})$
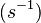
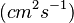
gamma : quenching coefficient. $(cm^{2}s^{-1})$
g : generation rate if you wanna let whole recombination rate change into exciton you should set g as 1.

Example

$callexciton
5
2e-14 20000 3000 1e-12 1
2e-14 20000 3000 1e-12 1
2e-14 20000 3000 1e-12 1
2e-14 20000 3000 1e-12 1
2e-14 20000 3000 1e-12 1

static TTA model (mode 7)

Format

$callexciton
20
7 1 1
DS DT krS knrS krT knrT kisc krisc keS khS keT khT kST gammaTS gammaTT a DrefS DrefT ES ET

Parameter Explanation ...

Output Format
*.1DexQE
V I Sr Snr Tr Tnr Sisc Tisc KeS KhS keT khT kts Sann TSA TTA sumSQE sumTQE

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

sumSQE+sumTQE should equal to 1.

Subroutine_exciton1D,

@@ 行 14： / 行 14： @@
 <big>2. Exciton Quenching: <math>[n^{T,S}_{1}\rightarrow n^{T,S}_{0}]</math></big>
-<math>(k_{r}+k_{nr})n_{ex}, [n_{ex}\rightarrow n_{ex}]</math></big>
+<big><math>(k_{r}+k_{nr})n_{ex}</math></big>
-<big>3. Singlet-Polaron Quenching: <math>(k_{e}^Sn+k_{h}^Sp)S, [S_1+n/p\rightarrow S_0+n/p^{*}]</math></big>
+<big>3. Singlet-Polaron Quenching: <math>[S_1+n/p\rightarrow S_0+n/p^{*}]</math></big>
+<big><math>(k_{e}^Sn+k_{h}^Sp)S</math></big>
 <big>4. Triplet-Polaron Quenching: <math>(k_{e}^Tn+k_{h}^Tp)T, [T_1+n/p\rightarrow S_0+n/p^{*}]</math></big>

"$callexciton" 修訂間的差異

於 2021年8月17日 (二) 10:52 的修訂

導覽選單

個人工具

命名空間

變體

檢視

更多

搜尋

導覽

工具