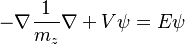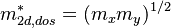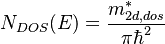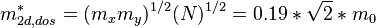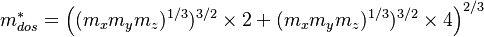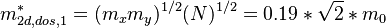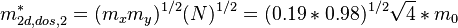"$1Daddefmas" 修訂間的差異

出自 DDCC TCAD TOOL Manual
前往： 導覽、 搜尋
 
(未顯示同一使用者於中間所作的 8 次修訂)
行 3： 行 3：
 
$1Daddefmas
  
$1Daddefmas
 
I_effective_type
 
I_effective_type
−
<math> m_{hh,z} ~~ m_{hh,x}~~ m_{hh,y}~~m_{lh,z} ~~ m_{lh,x}~~ m_{lh,y} ~~m_{e,z} ~~ m_{e,x}~~ m_{hh,y}~~N_{valley}..</math>
 +
<math> m_{hh,z} ~~ m_{hh,x}~~ m_{hh,y}~~N_{valley}~~\Delta E_{hh}~~m_{lh,z} ~~ m_{lh,x}~~ m_{lh,y}~~N_{valley}~~\Delta E_{lh}~~m_{e,z} ~~ m_{e,x}~~ m_{hh,y}~~N_{valley}~~\Delta E_{c1}..</math>
−
<math> m_{hh,z} ~~ m_{hh,x}~~ m_{hh,y}~~m_{lh,z} ~~ m_{lh,x}~~ m_{lh,y} ~~m_{e,z} ~~ m_{e,x}~~ m_{hh,y}~~N_{valley}..</math>
 +
<math> m_{hh,z} ~~ m_{hh,x}~~ m_{hh,y}~~N_{valley}~~\Delta E_{hh}~~m_{lh,z} ~~ m_{lh,x}~~ m_{lh,y}~~N_{valley}~~\Delta E_{lh}~~m_{e,z} ~~ m_{e,x}~~ m_{hh,y}~~N_{valley}..~~\Delta E_{c1}</math>
 
... to N layers
  
... to N layers
 
 
−
I_effective_type is the input type. The default should be 1. The typical semiconductor material has heavy hole, light hole, and electron effective mass of direct band. The type 1 is used.
+
I_effective_type is the input type. The default should be 1. The typical semiconductor material has a heavy hole, a light hole, and electron effective mass of a direct band. The type 1 is used.
−
For I_effective_type= 1, <math> m_{hh,z} ~~ m_{hh,x}~~ m_{hh,y}~~m_{lh,z} ~~ m_{lh,x}~~ m_{lh,y} ~~m_{e,z} ~~ m_{e,x}~~ m_{hh,y}~~ N_{valley}..</math>
 +
For I_effective_type= 1, m_{hh,z} ~~ m_{hh,x}~~ m_{hh,y}~~N_{valley}~~\Delta E_{hh}~~m_{lh,z} ~~ m_{lh,x}~~ m_{lh,y}~~N_{valley}~~\Delta E_{lh}~~m_{e,z} ~~ m_{e,x}~~ m_{hh,y}~~N_{valley}~~\Delta E_{c1}....</math>
−
For I_effective_type= 2, <math> m_{hh,z} ~~ m_{hh,x}~~ m_{hh,y}~~m_{lh,z} ~~ m_{lh,x}~~ m_{lh,y} ~~m_{e,z} ~~ m_{e,x}~~ m_{hh,y}~~ N_{valley}~~m_{e,z,2nd valley} ~~ m_{e,x,2nd valley}~~ m_{hh,y,2nd valley}~~ N_{valley}..</math>
 +
For I_effective_type= 2, <math> m_{hh,z} ~~ m_{hh,x}~~ m_{hh,y}~~N_{valley}~~\Delta E_{hh}~~m_{lh,z} ~~ m_{lh,x}~~ m_{lh,y}~~N_{valley}~~\Delta E_{lh}~~m_{e,z} ~~ m_{e,x}~~ m_{hh,y}~~N_{valley}~~\Delta E_{c1} ~~m_{e,z,2nd} ~~ m_{e,x,2nd}~~ m_{e,y,2nd}~~N_{valley,2nd}~~\Delta E_{c2}....</math>
  +
  +
Note: For type 2, it is designed for direct and indirect calculation in landscape cases.
   
 
z is the calculation direction of 1D program. If there is a QW, z is the confined direction in the 1D program. <math>N_{valley}</math> is the valley number of electrons
  
z is the calculation direction of 1D program. If there is a QW, z is the confined direction in the 1D program. <math>N_{valley}</math> is the valley number of electrons
行 17： 行 17：
 
$1Daddefmas
  
$1Daddefmas
 
1
 
1
−
1.8 1.8 1.8 0.17 0.17 0.17 0.21 0.2 0.2
 +
1.8 1.8 1.8 1 0.0 0.17 0.17 0.17 1 0.0 0.21 0.2 0.2 1 0.0
−
1.8 1.8 1.8 0.17 0.17 0.17 0.21 0.2 0.2
 +
1.8 1.8 1.8 1 0.0 0.17 0.17 0.17 1 0.0 0.21 0.2 0.2 1 0.0
−
1.8 1.8 1.8 0.17 0.17 0.17 0.21 0.2 0.2
+
1.8 1.8 1.8 1 0.0 0.17 0.17 0.17 1 0.0 0.21 0.2 0.2 1 0.0
 
.... to N layers
  
.... to N layers
   
−
For example, for a material effective mass for HH_growth direction is 1.4 in the other two directions are 0.7 and 0.9, LH=0.17, and electron is 0.21 in the growth direction and 0.2 in the x,y direction, we set
+
Example II: For a material like AlGaN effective mass for HH is 1.8, LH=0.17, and the electron is 0.21 in the growth direction and 0.2 in the x,y direction. If it is under strain and HH shifts to the top first band by <math>\Delta E_{hh} = 0.2 eV</math> (move up use positive sign),
  +
 
$1Daddefmas
  
$1Daddefmas
 
1
 
1
−
1.4 0.7 0.9 0.17 0.17 0.17 0.21 0.2 0.2
 +
1.8 1.8 1.8 1 '''0.2''' 0.17 0.17 0.17 1 0.0 0.21 0.2 0.2 1 0.0
−
1.4 0.7 0.9 0.17 0.17 0.17 0.21 0.2 0.2
 +
1.8 1.8 1.8 1 '''0.2''' 0.17 0.17 0.17 1 0.0 0.21 0.2 0.2 1 0.0
−
1.4 0.7 0.9 0.17 0.17 0.17 0.21 0.2 0.2
+
1.8 1.8 1.8 1 '''0.2''' 0.17 0.17 0.17 1 0.0 0.21 0.2 0.2 1 0.0
 
.... to N layers
  
.... to N layers
   
⚫
Actually, the simulation program, it mainly uses the density of state effective mass. The different direction's effective mass will be put together as
 
  +
For example, for a material effective mass for HH_growth direction is 1.4 in the other two directions are 0.7 and 0.9, LH=0.17, and electron is 0.3 in the growth direction and 0.1 in the x,y direction with 3 valleys, we set
  +
$1Daddefmas
  +
1
  +
1.4 0.7 0.9 1 0.0 0.17 0.17 0.17 1 0.0 0.3 0.1 0.1 3 0.0
  +
1.4 0.7 0.9 1 0.0 0.17 0.17 0.17 1 0.0 0.3 0.1 0.1 3 0.0
  +
1.4 0.7 0.9 1 0.0 0.17 0.17 0.17 1 0.0 0.3 0.1 0.1 3 0.0
  +
.... to N layers
  +
  ⚫
Actually, the simulation program mainly uses the density of state effective mass. The different direction's effective mass will be put together as
 
For conduction band:
  
For conduction band:
 
<math> m_{dos}^{*} = (N_{valley})^{2/3} ( m_x m_y m_z)^{1/3} </math>
  
<math> m_{dos}^{*} = (N_{valley})^{2/3} ( m_x m_y m_z)^{1/3} </math>
行 41： 行 49：
 
For the Schrodinger solver, it will use m_z to calculate the quantum confinement effects. The equation will solve
  
For the Schrodinger solver, it will use m_z to calculate the quantum confinement effects. The equation will solve
 
<math> {- \nabla \frac{1}{m_{z}} \nabla + V } \psi = E \psi </math>
  
<math> {- \nabla \frac{1}{m_{z}} \nabla + V } \psi = E \psi </math>
−
The for the n2d calculation, the density of state effective mass in the 2D structures is
 +
For the n2d calculation, the density of state effective mass in the 2D structures is
 
<math> m_{2d,dos}^{*} = ( m_{x} m_{y} ) ^{1/2} </math>
  
<math> m_{2d,dos}^{*} = ( m_{x} m_{y} ) ^{1/2} </math>
−
<math> N_DOS(E) = \frac{m_{2d,dos}^{*}}{\pi\hbar^{2}}</math>
 +
<math> N_{DOS}(E) = \frac{m_{2d,dos}^{*}}{\pi\hbar^{2}}</math>
  +
  +
For structures like Si, it may have some problems when the Schrodinger solver is used. Since Si has six valleys with effective masses in different directions (<math>m_{l}=0.98 m_{0}, m_{l}=0.19 m_{0}</math>, if we do not solve the Schrodinger equations, we can simply use m_e =1.08 m0 in the $1Dparameter. Or here, we can set
  +
$1Daddefmas
  +
1
  +
0.49 0.49 0.49 1 0.0 0.16 0.16 0.16 1 0.0 '''0.98 0.19 0.19 6 0.0'''
  +
  +
For the Schrodinger solver, after quantum confined effects, we can expect two confinement in the electron effective mass, the lower valleys are z valleys with mz=0.98, N=2. We can neglect the high valleys, and only two valleys are left as ground states. The setting would be
  +
  +
$1Daddefmas
  +
1
  +
0.49 0.49 0.49 0.16 0.0 0.16 0.16 0.98 0.0 0.19 0.19 2 0.0
  +
  +
<math> m_{2d,dos}^{*} = ( m_{x} m_{y} ) ^{1/2} (N)^{1/2}= 0.19 * \sqrt{2} * m_{0} </math>
  +
<math> N_{DOS}(E) = \frac{m_{2d,dos}^{*}}{\pi\hbar^{2}}</math>
  +
If we want to use type 2 to consider the second confine states, we can set ( Note x and y is undistinguished in 1D simulation program as they will be treated together)
  +
  +
$1Daddefmas
  +
2
  +
0.49 0.49 0.49 1 0.0 0.16 0.16 0.16 1 0.0 '''0.98 0.19 0.19 2 0.0 0.19 0.98 0.19 4 0.0'''
  +
  +
For unconfined conditions, it will set the mass of the electron to be
  +
<math> m_{dos}^{*} = \left( (m_x m_y m_z)^{1/3})^{3/2} \times 2 + (m_x m_y m_z)^{1/3})^{3/2} \times 4 \right)^{2/3} </math>
  +
  +
For the confined conditions, it will
  +
<math> m_{2d,dos,1}^{*} = ( m_{x} m_{y} ) ^{1/2} (N)^{1/2}= 0.19 * \sqrt{2} * m_{0} </math>
  +
<math> m_{2d,dos,2}^{*} = ( m_{x} m_{y} ) ^{1/2} (N)^{1/2}= (0.19 * 0.98)^{1/2} \sqrt{4} * m_{0} </math>
  +
  +
For the In0.5Ga0.5P material, which has a 2nd valley (X) close to Gamma valley. In addition, the QB is usually dominated by X valley, which is an indirect bandgap. To solve Schrodinger equations, it is better to solve <math>\Gamma </math> valley and X separately. For Example, In0.5Ga0.5P is the direct bandgap X valley is above the <math>\Gamma </math> valley around 0.2eV, AlInP is the indirect bandgap, where X valley is below <math>\Gamma </math> valley about 0.4eV. Then we can use type 2 and set the first Ec as <math>\Gamma </math> valley and the 2nd Ec as X valley. Then
  +
  +
  +
$1Daddefmas
  +
2
  +
0.49 0.49 0.49 1 0.0 0.16 0.16 0.16 1 0.0 '''0.08 0.08 0.08 1 0.0 0.98 0.19 0.19 3 0.2''' -> InGaP
  +
0.49 0.49 0.49 1 0.0 0.16 0.16 0.16 1 0.0 '''0.098 0.098 0.098 1 0.4 0.94 0.21 0.21 3 0.0''' -> AlInP

於 2023年3月11日 (六) 15:59 的最新修訂

$1Daddefmas   is the function to add additional effective mass information for electron and holes. In some cases, the electron's (holes) effective mass in different directions are different. Hence the new functions is to put additional information for the program to calculate. 

$1Daddefmas
I_effective_type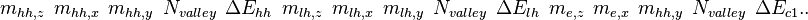 
 m_{hh,z} ~~ m_{hh,x}~~ m_{hh,y}~~N_{valley}~~\Delta E_{hh}~~m_{lh,z} ~~ m_{lh,x}~~ m_{lh,y}~~N_{valley}~~\Delta E_{lh}~~m_{e,z} ~~ m_{e,x}~~ m_{hh,y}~~N_{valley}~~\Delta E_{c1}..
 m_{hh,z} ~~ m_{hh,x}~~ m_{hh,y}~~N_{valley}~~\Delta E_{hh}~~m_{lh,z} ~~ m_{lh,x}~~ m_{lh,y}~~N_{valley}~~\Delta E_{lh}~~m_{e,z} ~~ m_{e,x}~~ m_{hh,y}~~N_{valley}..~~\Delta E_{c1}
... to N layers

I_effective_type is the input type. The default should be 1. The typical semiconductor material has a heavy hole, a light hole, and electron effective mass of a direct band. The type 1 is used. 
For I_effective_type= 1, m_{hh,z} ~~ m_{hh,x}~~ m_{hh,y}~~N_{valley}~~\Delta E_{hh}~~m_{lh,z} ~~ m_{lh,x}~~ m_{lh,y}~~N_{valley}~~\Delta E_{lh}~~m_{e,z} ~~ m_{e,x}~~ m_{hh,y}~~N_{valley}~~\Delta E_{c1}....</math>
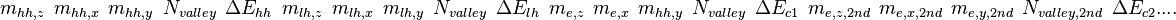
For I_effective_type= 2,  m_{hh,z} ~~ m_{hh,x}~~ m_{hh,y}~~N_{valley}~~\Delta E_{hh}~~m_{lh,z} ~~ m_{lh,x}~~ m_{lh,y}~~N_{valley}~~\Delta E_{lh}~~m_{e,z} ~~ m_{e,x}~~ m_{hh,y}~~N_{valley}~~\Delta E_{c1} ~~m_{e,z,2nd} ~~ m_{e,x,2nd}~~ m_{e,y,2nd}~~N_{valley,2nd}~~\Delta E_{c2}....

Note: For type 2, it is designed for direct and indirect calculation in landscape cases. 

z is the calculation direction of 1D program. If there is a QW, z is the confined direction in the 1D program. N_{valley} is the valley number of electrons

For example, for a material like GaN effective mass for HH is 1.8, LH=0.17, and the electron is 0.21 in the growth direction and 0.2 in the x,y direction. We set 

 $1Daddefmas
 1 
 1.8 1.8 1.8 1 0.0 0.17 0.17 0.17 1 0.0 0.21 0.2 0.2 1 0.0 
 1.8 1.8 1.8 1 0.0 0.17 0.17 0.17 1 0.0 0.21 0.2 0.2 1 0.0 
 1.8 1.8 1.8 1 0.0 0.17 0.17 0.17 1 0.0 0.21 0.2 0.2 1 0.0 
 .... to N layers

Example II: For a material like AlGaN effective mass for HH is 1.8, LH=0.17, and the electron is 0.21 in the growth direction and 0.2 in the x,y direction. If it is under strain and HH shifts to the top first band by 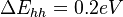\Delta E_{hh} = 0.2 eV (move up use positive sign), 

 $1Daddefmas
 1 
 1.8 1.8 1.8 1 0.2 0.17 0.17 0.17 1 0.0 0.21 0.2 0.2 1 0.0 
 1.8 1.8 1.8 1 0.2 0.17 0.17 0.17 1 0.0 0.21 0.2 0.2 1 0.0 
 1.8 1.8 1.8 1 0.2 0.17 0.17 0.17 1 0.0 0.21 0.2 0.2 1 0.0 
 .... to N layers

For example, for a material effective mass for HH_growth direction is 1.4 in the other two directions are 0.7 and 0.9, LH=0.17, and electron is 0.3 in the growth direction and 0.1 in the x,y direction with 3 valleys, we set 

 $1Daddefmas
 1 
 1.4 0.7 0.9 1 0.0 0.17 0.17 0.17 1 0.0 0.3 0.1 0.1 3 0.0 
 1.4 0.7 0.9 1 0.0 0.17 0.17 0.17 1 0.0 0.3 0.1 0.1 3 0.0
 1.4 0.7 0.9 1 0.0 0.17 0.17 0.17 1 0.0 0.3 0.1 0.1 3 0.0 
 .... to N layers

Actually, the simulation program mainly uses the density of state effective mass. The different direction's effective mass will be put together as 

For conduction band: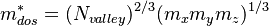
  m_{dos}^{*} = (N_{valley})^{2/3} ( m_x m_y m_z)^{1/3} 

For the valence band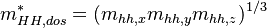 
   m_{HH, dos}^{*} = ( m_{hh,x} m_{hh,y} m_{hh,z})^{1/3}  
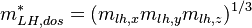
   m_{LH, dos}^{*} = ( m_{lh,x} m_{lh,y} m_{lh,z})^{1/3}  
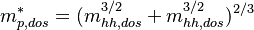
   m_{p, dos}^{*} = ( m_{hh,dos}^{3/2}+ m_{hh,dos}^{3/2} ) ^{2/3}

For the Schrodinger solver, it will use m_z to calculate the quantum confinement effects. The equation will solve 

 {- \nabla \frac{1}{m_{z}} \nabla + V } \psi = E \psi

For the n2d calculation, the density of state effective mass in the 2D structures is 

   m_{2d,dos}^{*} = ( m_{x} m_{y} ) ^{1/2} 
   N_{DOS}(E) = \frac{m_{2d,dos}^{*}}{\pi\hbar^{2}}

For structures like Si, it may have some problems when the Schrodinger solver is used. Since Si has six valleys with effective masses in different directions (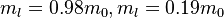m_{l}=0.98 m_{0}, m_{l}=0.19 m_{0}, if we do not solve the Schrodinger equations, we can simply use m_e =1.08 m0 in the $1Dparameter. Or here, we can set 

 $1Daddefmas
 1 
 0.49 0.49 0.49 1 0.0 0.16 0.16 0.16 1 0.0 0.98 0.19 0.19 6 0.0

For the Schrodinger solver, after quantum confined effects, we can expect two confinement in the electron effective mass, the lower valleys are z valleys with mz=0.98, N=2. We can neglect the high valleys, and only two valleys are left as ground states. The setting would be 

 $1Daddefmas
 1 
 0.49 0.49 0.49 0.16 0.0 0.16 0.16 0.98 0.0 0.19 0.19 2 0.0

   m_{2d,dos}^{*} = ( m_{x} m_{y} ) ^{1/2} (N)^{1/2}= 0.19 * \sqrt{2} * m_{0} 
   N_{DOS}(E) = \frac{m_{2d,dos}^{*}}{\pi\hbar^{2}}

If we want to use type 2 to consider the second confine states, we can set ( Note x and y is undistinguished in 1D simulation program as they will be treated together) 

 $1Daddefmas
 2 
 0.49 0.49 0.49 1 0.0 0.16 0.16 0.16 1 0.0 0.98 0.19 0.19 2 0.0 0.19 0.98 0.19 4 0.0

For unconfined conditions, it will set the mass of the electron to be 

   m_{dos}^{*} = \left(  (m_x m_y m_z)^{1/3})^{3/2} \times 2 +  (m_x m_y m_z)^{1/3})^{3/2}  \times 4  \right)^{2/3}

For the confined conditions, it will 

   m_{2d,dos,1}^{*} = ( m_{x} m_{y} ) ^{1/2} (N)^{1/2}= 0.19 * \sqrt{2} * m_{0} 
   m_{2d,dos,2}^{*} = ( m_{x} m_{y} ) ^{1/2} (N)^{1/2}= (0.19 * 0.98)^{1/2} \sqrt{4} * m_{0}

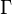For the In0.5Ga0.5P material, which has a 2nd valley (X) close to Gamma valley. In addition, the QB is usually dominated by X valley, which is an indirect bandgap. To solve Schrodinger equations, it is better to solve \Gamma valley and X separately. For Example, In0.5Ga0.5P is the direct bandgap X valley is above the \Gamma valley around 0.2eV, AlInP is the indirect bandgap, where X valley is below 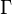\Gamma valley about 0.4eV. Then we can use type 2 and set the first Ec as 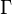\Gamma valley and the 2nd Ec as X valley. Then 


 $1Daddefmas
 2 
 0.49 0.49 0.49 1 0.0 0.16 0.16 0.16 1 0.0 0.08 0.08 0.08 1 0.0 0.98 0.19 0.19 3 0.2    -> InGaP
 0.49 0.49 0.49 1 0.0 0.16 0.16 0.16 1 0.0 0.098 0.098 0.098 1 0.4 0.94 0.21 0.21 3 0.0    -> AlInP
取自 "http://yrwu-wk.ee.ntu.edu.tw/mediawiki/index.php?title=$1Daddefmas&oldid=2676"