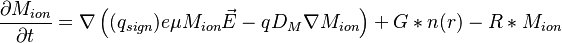"$Withionmove" 修訂間的差異
出自 DDCC TCAD TOOL Manual
| 行 1: | 行 1: | ||
When the system has ion to perform as drift-diffusion equations, we solve the time dependent drift-diffusion for slow ion move simulation. Since the ion moves may not be governed fermi-level concept. We simply treat is a tradiational drift-diffusion equations. |
When the system has ion to perform as drift-diffusion equations, we solve the time dependent drift-diffusion for slow ion move simulation. Since the ion moves may not be governed fermi-level concept. We simply treat is a tradiational drift-diffusion equations. |
||
<br> |
<br> |
||
| − | <math> \frac{\partial M_{ion}}{\partial t} = \nabla \left( (q_{sign}) e\mu M_{ion} \vec{E} - q D_{M} \nabla M_{ion} \right)</math> |
+ | <math> \frac{\partial M_{ion}}{\partial t} = \nabla \left( (q_{sign}) e\mu M_{ion} \vec{E} - q D_{M} \nabla M_{ion} \right) + G*n(r) - R*M_{ion} </math> |
Ideally, the ion density is given by initial setting. The total ion number should be fixed. The program is aim to model multi-ions drift-diffusion. The command is as following. |
Ideally, the ion density is given by initial setting. The total ion number should be fixed. The program is aim to model multi-ions drift-diffusion. The command is as following. |
||
於 2023年10月3日 (二) 16:41 的修訂
When the system has ion to perform as drift-diffusion equations, we solve the time dependent drift-diffusion for slow ion move simulation. Since the ion moves may not be governed fermi-level concept. We simply treat is a tradiational drift-diffusion equations.
Ideally, the ion density is given by initial setting. The total ion number should be fixed. The program is aim to model multi-ions drift-diffusion. The command is as following.
$Withionmove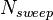
Sweep_type_1
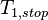
P1 P2 P3 P4 P5 ... Sweep_type_1
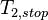
P1 P2 P3 P4 P5 .. ... ... Sweep_type_N_{sweep
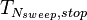
P1 P2 P3 P4 P5 ..
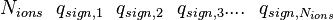
p3 p4 Parameters of the 1 layer
p3 p4 Parameters of the 2 layer
p3 p4 Parameters of the 3 layer .... .....
p3 p4 Parameters of the $totalregion layer
: The number of runs for the time step
: The number of output results for each run Sweep_type: 1: constant voltage, P1 to P5 is not used 2: Sweep Vg during this time period P1=Vgstart, P2=Vgend, P3=swdt of each step (step Number=
3: Sweep Vd during this time period P1=Vdstart, P2=Vdend, P3=swdt of each step 4,5,6.... leave for future use
: The time for the first run.
The time for the 2nd run.
is the
for each sweep.
How many ions are considered. If we only want to consider 1 negative ion,we can put 1
The sign of ions. only accept
For example: Consider 2 ions, 1st is negative charges, 2nd is positive charges, total 5 Regions we can
$Withionmove 3 1000 1 1.00 1.0d-4 3 1.00 1.0d-4 0.0 1.0 0.02 1 1.00 1.0d-4 2 -1.0 1.0 1 0.0e17 0.0 0.0e17 0.0 1 1.0e17 1.0e-11 2.0e17 1.0e-12 1 1.0e17 1.0e-11 2.0e17 1.0e-12 1 1.0e17 1.0e-11 2.0e17 1.0e-12 1 1.0e17 1.0e-11 2.0e17 1.0e-12
is the parameter type: it depends on ion number
1:
,
,........
2:
,
,........
3:
,
,........
4:
,
,........
5:
,
,........
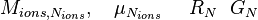
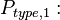
When type 1 is chosen, we only put mobility
, and the diffusion coefficient
is calculated with Einstein relation, where
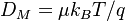
When type 2 is chosen, the diffusion coefficient is given by input
For type==3, the ion mobility, quench term for R, Generation term for G is provided.
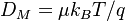
For type==4, the ion mobility, diffusion coefficients, quench term for R, Generation term for G is provided.
For type==5, the ion mobility, quench term for R, Generation term for G is provided.
The initial ion density is provided by traps in the steady state calculation.
See related commands
Related commands: $Withionmove $IonMovewithPoisson *.time_ion