"$xgradualdiv" 修訂間的差異
出自 DDCC TCAD TOOL Manual
| (未顯示由 2 位使用者於中間所作的 2 次修訂) | |||
| 行 51： | 行 51： | ||
<br> |
<br> |
||
: Example |
: Example |
||
| + | $xnode |
||
| + | 0.0 |
||
| + | 20.0 |
||
| + | 40.0 |
||
| + | 60.0 |
||
| + | |||
| + | $xdiv |
||
| + | 30 |
||
| + | 70 |
||
| + | 80 |
||
| + | |||
$xgradualdiv |
$xgradualdiv |
||
| − | 0 |
+ | 0 |
1 1.1 |
1 1.1 |
||
| − | + | 2 0.95 |
|
| − | + | ||
| − | + | <br>'''<big><big>The $xgradualdiv setting in GUI interface is here</big></big>''' <br> |
|
| + | 1. After setting up the X-nodes, press '''Edit the nodes'''.<br> |
||
| + | 2. Choose the 1<sup>st</sup> node and set the Method to '''Uniform''' with a Mesh ratio of 0.00.<br> |
||
| + | [[檔案:2D_xgradualdiv_fig1.jpg|1200px]]<br><br> |
||
| + | 3. Choose the 2<sup>nd</sup> node and set the Method to '''Gradual change''' with a Mesh ratio of 1.10.<br> |
||
| + | [[檔案:2D_xgradualdiv_fig2.jpg|1200px]]<br><br> |
||
| + | 4. Choose the 3<sup>rd</sup> node and set the Method to '''Bump''' with a Mesh ratio of 0.95.<br> |
||
| + | [[檔案:2D_xgradualdiv_fig3.jpg|1200px]]<br><br> |
||
| + | [[檔案:2D_xgradualdiv_fig4.jpg|1200px]] |
||
<br><br> |
<br><br> |
||
: Related commands |
: Related commands |
||
| − | :; [[$ygradualdiv]] |
+ | :; [[$ygradualdiv]] , [[$xnode]],[[$xdiv]] |
於 2024年10月21日 (一) 17:38 的最新修訂
This function is to determine how the segment is divided. There are two columns to fill in. The first column i should be filled in an integer 0, 1, or 2.
i = 0: Uniform. This means the segment is divided equally with the same spacing. i = 1: Gradual. This means the segment is divided whether from small spacing to large spacing or in the opposite way. The spacing is distributed like a geometric progression i = 2: Bump. This means the segment can be divided into two forms small-large-small or large-small-large.
The second column r should be filled in a real number.
| If r < 1 | If r = 1 | If r > 1 | |
|---|---|---|---|
| Uniform (0) | uniform | uniform | uniform |
| Gradual (1) | large -> small | uniform | small -> large |
| Bump (2) | large -> small -> large | uniform | small -> large -> small |
If the total layer thickness isand i=1, then if the smallest separation distance is a
where N is the total grid number defined in $xdiv Then
If the total layer thickness iswhere N is the total grid number defined in $ydiv Then
- Example
$xnode 0.0 20.0 40.0 60.0 $xdiv 30 70 80 $xgradualdiv 0 1 1.1 2 0.95
The $xgradualdiv setting in GUI interface is here
1. After setting up the X-nodes, press Edit the nodes.
2. Choose the 1st node and set the Method to Uniform with a Mesh ratio of 0.00.
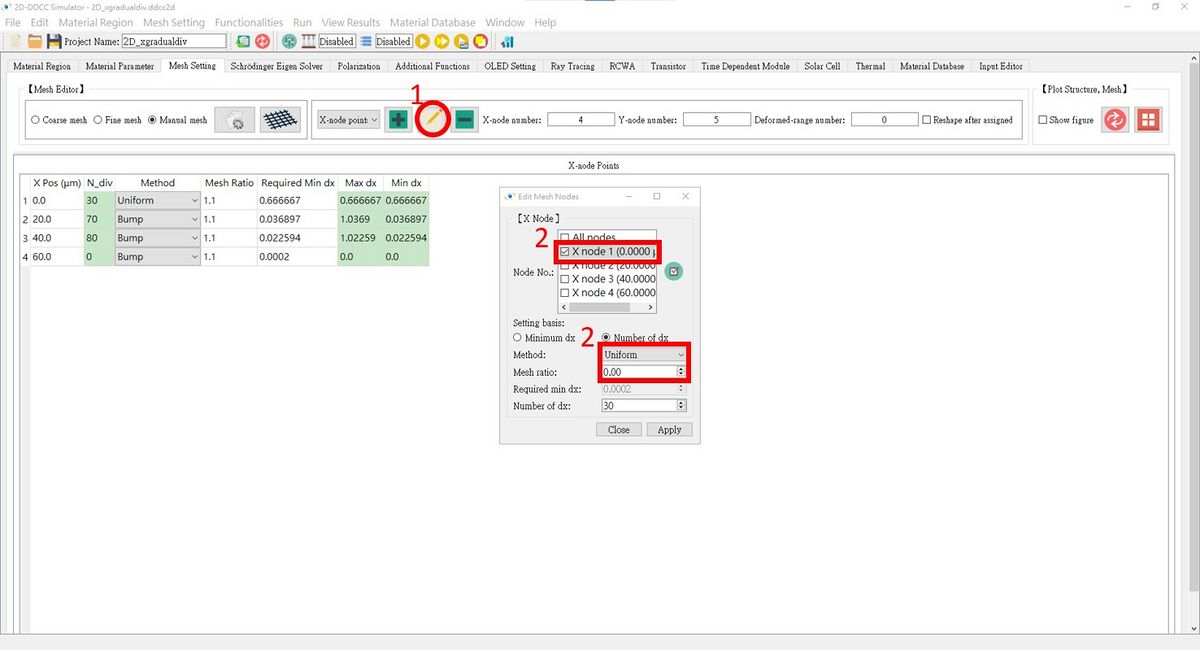
3. Choose the 2nd node and set the Method to Gradual change with a Mesh ratio of 1.10.
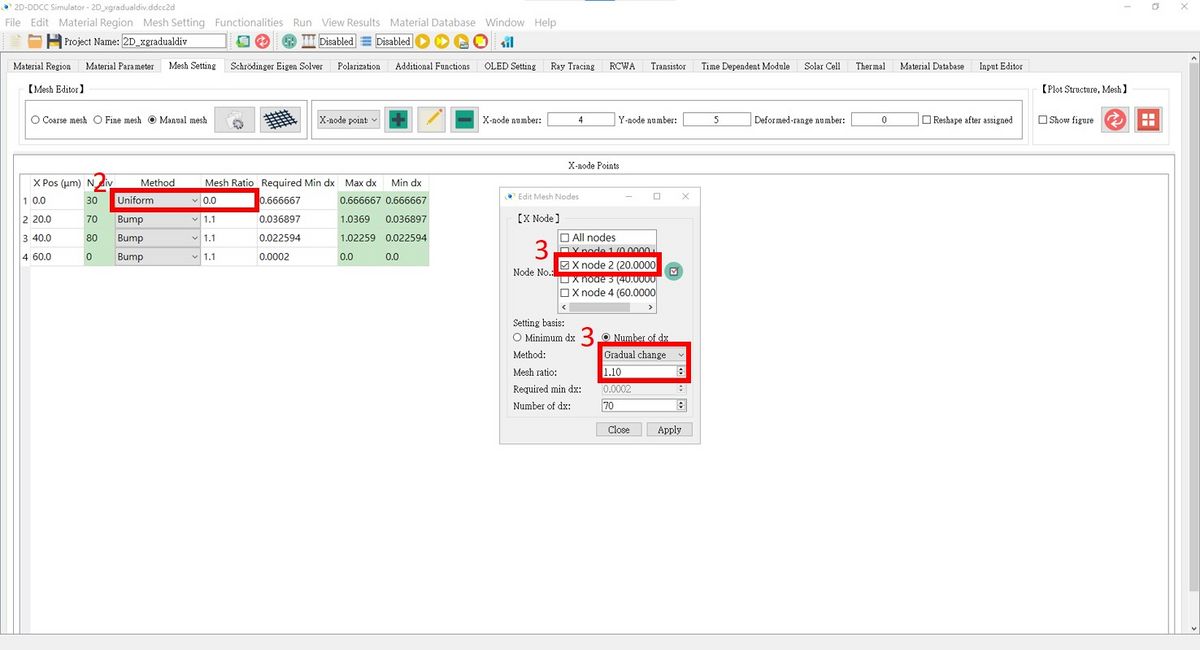
4. Choose the 3rd node and set the Method to Bump with a Mesh ratio of 0.95.
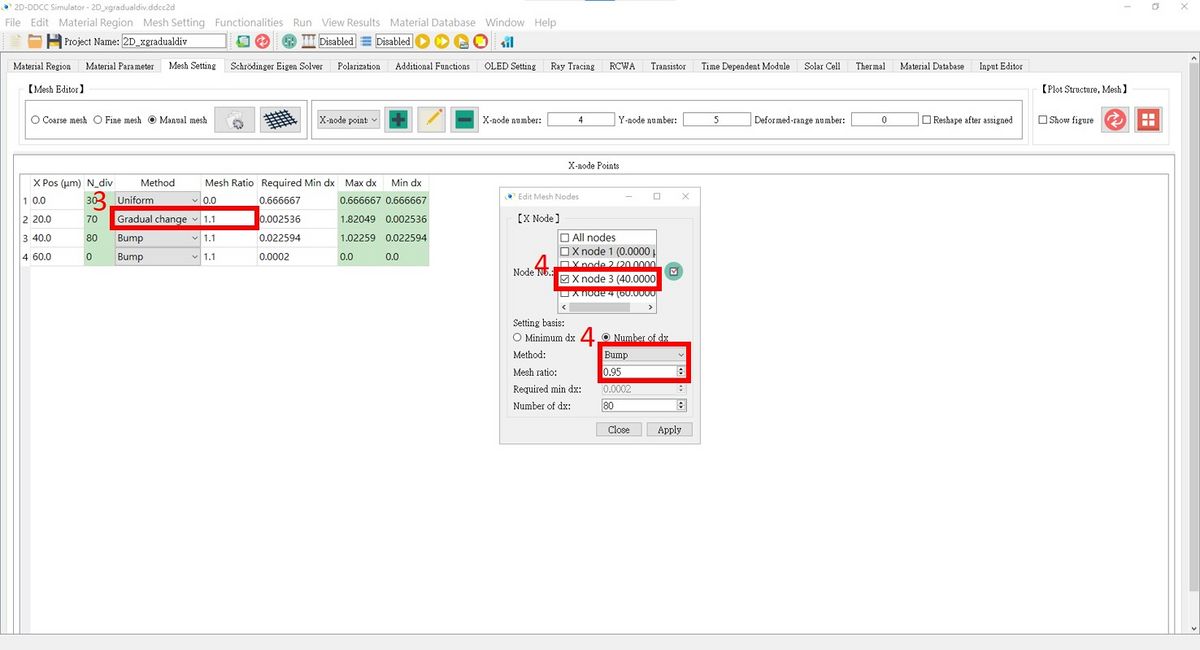
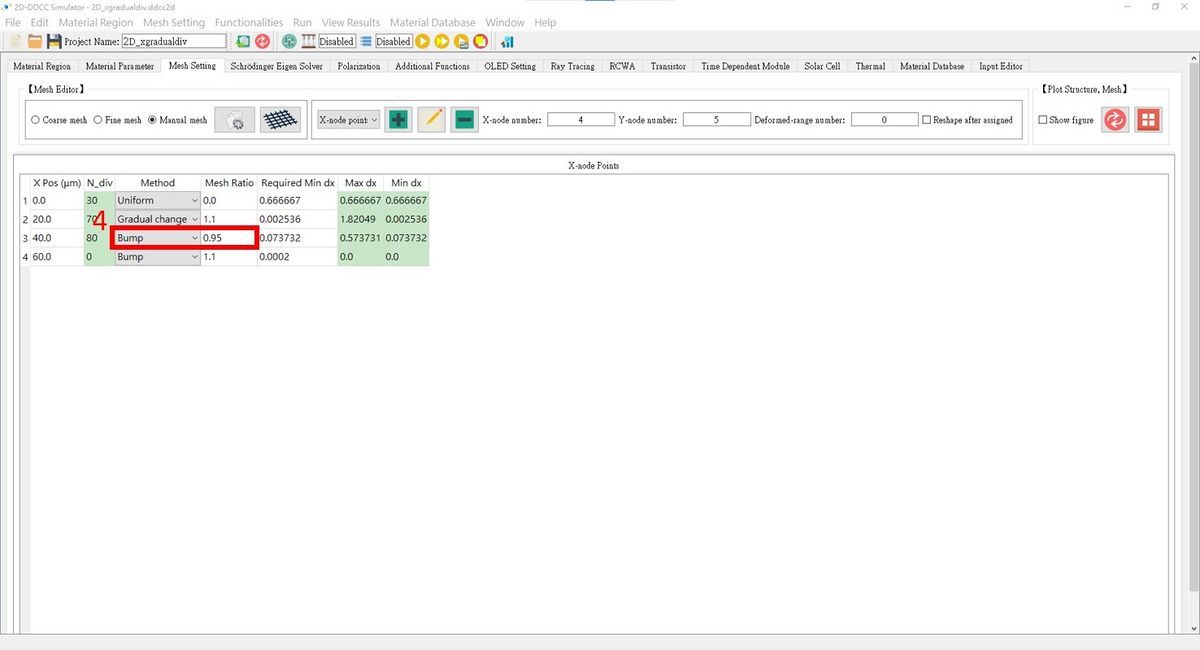
- Related commands
