"Solvetimestep2D" 修訂間的差異

出自 DDCC TCAD TOOL Manual
前往： 導覽、 搜尋
(已建立頁面，內容為 "$solvetimestep is a command for solving the transient behavior of the device. The format is $solvetimestep2D number_of_different_steps(Nt) steptype contact_type...")
 
 
(未顯示由 1 位使用者於中間所作的 11 次修訂)
行 1： 行 1：
−
$solvetimestep is a command for solving the transient behavior of the device. The format is
+
$solvetimestep2D is a command for solving the transient behavior of the device. The format is
   
 
$solvetimestep2D
  
$solvetimestep2D
行 13： 行 13：
 
Steptype = 1: <br>
  
Steptype = 1: <br>
 
<math>\delta t,~~ t_{total},~~ vg_0 </math><br>
  
<math>\delta t,~~ t_{total},~~ vg_0 </math><br>
−
vg=vg_end for t<0, for t>0, vg=<math> vg_0 </math><br>
 +
<math>vg=vg_{end}</math> for t<0, for t>0, vg=<math> vg_0 </math><br>
   
 
Steptype = 2: <br>
  
Steptype = 2: <br>
 
<math>\delta t,~~ t_{total},~~ vg_0 ,~~ A_{0} ,~~ \omega,~~ c_{0} </math><br>
  
<math>\delta t,~~ t_{total},~~ vg_0 ,~~ A_{0} ,~~ \omega,~~ c_{0} </math><br>
−
<math> vg=vg_0 + A_{0} \times sin\left( 2\pi \omega t + c_0 \right) </math><br>
 +
<math> vg=vg_{0} + A_{0} \times sin\left( 2\pi \omega t + c_0 \right) </math><br>
   
 
Steptype = 3: <br>
  
Steptype = 3: <br>
 
<math>\delta t, ~~t_{total},~~ vg_0 ,~~ A_{0} ,~~ \omega ,~~ c_{0} </math><br>
  
<math>\delta t, ~~t_{total},~~ vg_0 ,~~ A_{0} ,~~ \omega ,~~ c_{0} </math><br>
−
<math> vg=vg_0 + int(A_{0} \times sin\left( 2\pi \omega t + c_0 \right)) </math><br>
 +
<math> vg=vg_{0} + int(A_{0} \times sin\left( 2\pi \omega t + c_0 \right)) </math><br>
   
 
contact_type
 
contact_type
行 27： 行 27：
 
3: source
  
3: source
 
4: drain
  
4: drain
  +
  +
Steptype = 4: <br>
  +
<math>\delta t,~~ t_{total},~~ vg_0 </math><br>
  +
<math>vg=vg_{end}</math> for t<0, for t>0, vg=<math> vg_0 </math> , generation = system generation at t<0 and generation =0 for t> 0 <br>
  +
  +
Steptype = 5: <br>
  +
<math>\delta t,~~ t_{total},~~ vg_0 ,~~ \omega ,~~ c_{0}</math><br>
  +
<math>vg=vg_{end}</math> for t<0, for t>0, vg=<math> vg_0 </math> , generation = system generation at t<0 generation = gen(system)*<math> (0.5+0.5*cos (2\pi \omega t + c_{0})) </math> <br>
  +
  +
Steptype = 6: <br>
  +
<math>\delta t,~~ t_{total},~~ vg_0 ,~~ \omega ,~~ c_{0}</math><br>
  +
<math>vg=vg_{end}</math> for t<0, for t>0, vg=<math> vg_0 </math> , generation = system generation at t<0 generation = gen(system)*<math> Int(0.5+0.5*cos (2\pi \omega t + c_{0})) </math> <br>
  +
  +
Steptype = 7: <br>
  +
<math>\delta t,~~ t_{total},~~ vg_0 ,~~ \omega ,~~ c_{0}</math><br>
  +
<math>vg=vg_{end}</math> for t<0, for t>0, vg=<math> vg_0 </math> , generation = 0 at t<0 (Force Steady state to be 0),
  +
generation = gen(system)*<math> (0.5+0.5*cos (2\pi \omega t + c_{0})) </math> <br>
  +
  +
Steptype = 8: <br>
  +
<math>\delta t,~~ t_{total},~~ vg_0 ,~~ \omega ,~~ c_{0}</math><br>
  +
<math>vg=vg_{end}</math> for t<0, for t>0, vg=<math> vg_0 </math> , generation = 0 at t<0 (Force Steady state to be 0),
  +
generation =gen(system)*<math> Int(0.5+0.5*cos (2\pi \omega t + c_{0})) </math> <br>
  +
  +
   
 
For example: <br>
 
For example: <br>
行 36： 行 60：
 
<math> vg=3.0 + 0.1 \times sin\left( 2\pi \times 10^{6} t \right) </math><br>
  
<math> vg=3.0 + 0.1 \times sin\left( 2\pi \times 10^{6} t \right) </math><br>
 
<math> vd=3.0 + 0.1 \times sin\left( 2\pi \times 10^{6} t \right) </math><br>
  
<math> vd=3.0 + 0.1 \times sin\left( 2\pi \times 10^{6} t \right) </math><br>
  +
  +
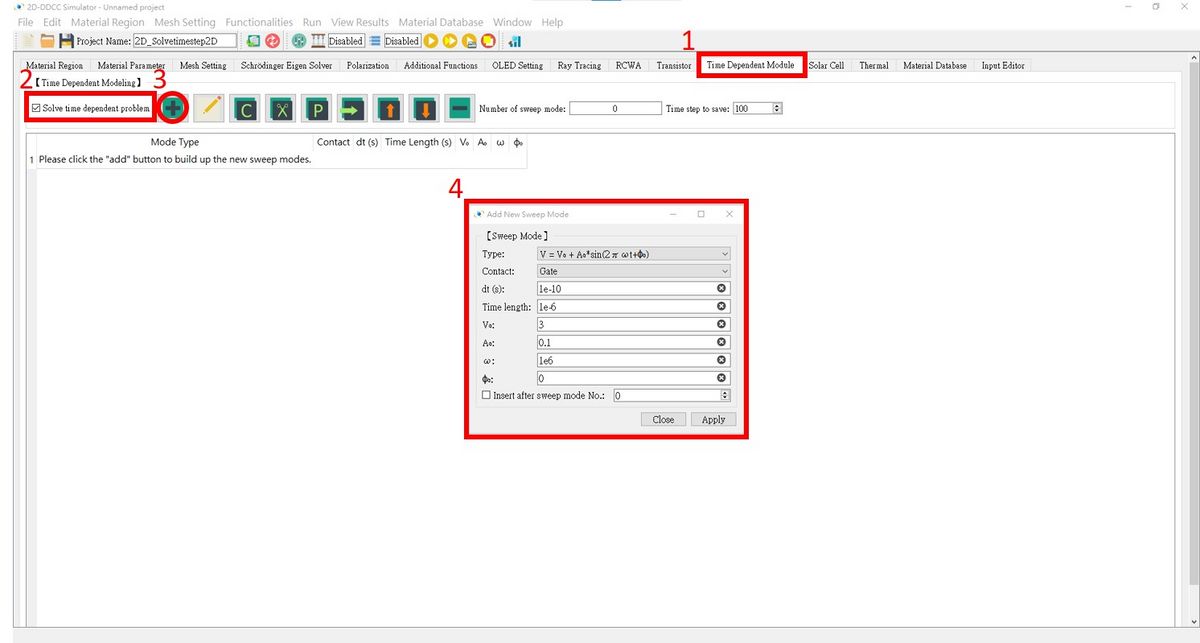
<br>'''<big><big>The $Solvetimestep2D setting in GUI interface is here</big></big>''' <br>
  +
1. Press '''Time Dependent module''', check the box and press '''Add new sweep modes'''.<br>
  +
2. Fill in the fields as needed!<br>
  +
[[檔案:2D_Solvetimestep2D_fig1.jpg|1200px]]<br>
  +
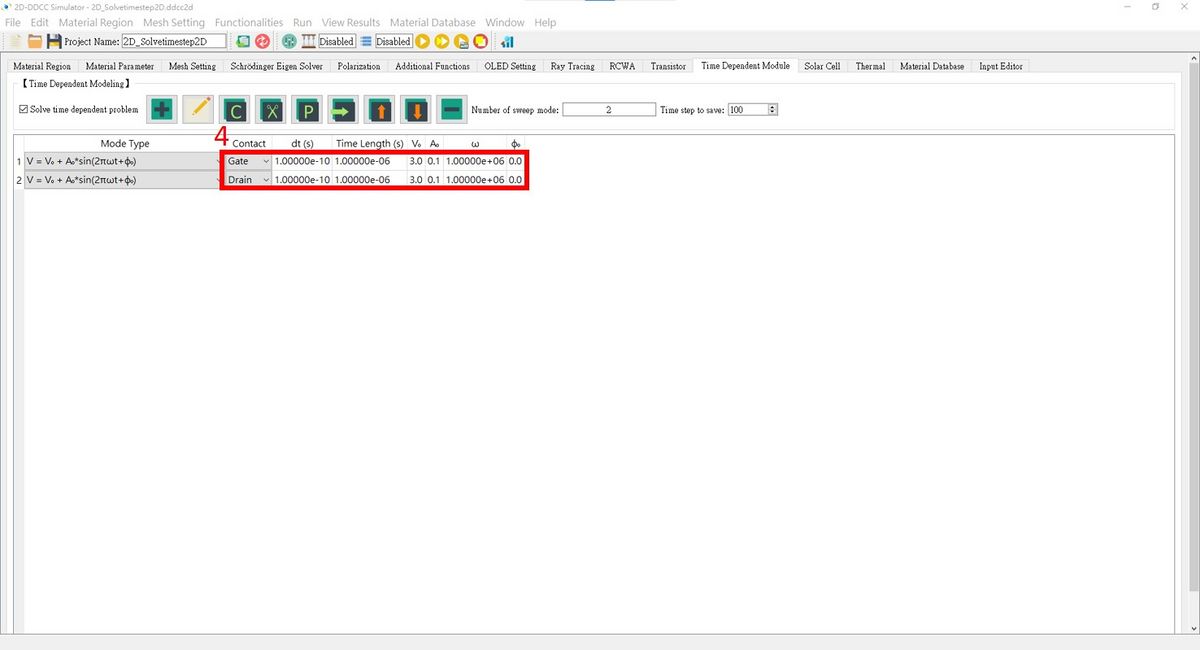
[[檔案:2D_Solvetimestep2D_fig2.jpg|1200px]]<br>
  +
  +
  +
related:<br>
  +
$[[savetimestep2D]]

於 2024年11月20日 (三) 19:43 的最新修訂

$solvetimestep2D is a command for solving the transient behavior of the device. The format is 

$solvetimestep2D
number_of_different_steps(Nt)
steptype contact_type \delta t ~~   t_{total} par1 par2 par3 par4 ....    
steptype contact_type \delta t ~~   t_{total} par1 par2 par3 par4 ....    
...
steptype contact_type \delta t ~~   t_{total} par1 par2 par3 par4 ....    repeat Nt times


The number of parameters depeding on step type. Now we have 3 step types 

Steptype  = 1:  

\delta t,~~ t_{total},~~ vg_0 

 vg=vg_{end} for t<0, for t>0, vg= vg_0  


Steptype  = 2:  

\delta t,~~ t_{total},~~ vg_0 ,~~ A_{0} ,~~ \omega,~~ c_{0} 

 vg=vg_{0} +  A_{0} \times sin\left( 2\pi \omega t + c_0 \right) 


Steptype  = 3:  

\delta t, ~~t_{total},~~ vg_0 ,~~  A_{0} ,~~ \omega ,~~ c_{0}  

 vg=vg_{0} +  int(A_{0} \times sin\left( 2\pi \omega t + c_0 \right))

contact_type 

2: gate
3: source
4: drain

Steptype  = 4:  

\delta t,~~ t_{total},~~ vg_0 

vg=vg_{end} for t<0, for t>0, vg= vg_0   , generation = system generation at t<0 and generation =0 for t> 0 
 

Steptype  = 5:  

\delta t,~~ t_{total},~~ vg_0 ,~~ \omega ,~~ c_{0}

vg=vg_{end} for t<0, for t>0, vg= vg_0   , generation = system generation at t<0 generation = gen(system)* (0.5+0.5*cos (2\pi \omega t + c_{0}))  
 

Steptype  = 6:  

\delta t,~~ t_{total},~~ vg_0 ,~~ \omega ,~~ c_{0}

vg=vg_{end} for t<0, for t>0, vg= vg_0   , generation = system generation at t<0 generation = gen(system)* Int(0.5+0.5*cos (2\pi \omega t + c_{0}))  
 

Steptype  = 7:  

\delta t,~~ t_{total},~~ vg_0 ,~~ \omega ,~~ c_{0}

vg=vg_{end} for t<0, for t>0, vg= vg_0   , generation = 0 at t<0 (Force Steady state to be 0), 
generation = gen(system)* (0.5+0.5*cos (2\pi \omega t + c_{0}))  
 

Steptype  = 8:  

\delta t,~~ t_{total},~~ vg_0 ,~~ \omega ,~~ c_{0}

vg=vg_{end} for t<0, for t>0, vg= vg_0   , generation = 0 at t<0 (Force Steady state to be 0),
generation =gen(system)* Int(0.5+0.5*cos (2\pi \omega t + c_{0}))


For example: 

$solvetimestep2D
2
2 2 1.0e-10 1.0e-6 3.00 0.1 1.0e6 0.0 
2 4 1.0e-10 1.0e-6 3.00 0.1 1.0e6 0.0 
  vg=3.0 + 0.1 \times sin\left( 2\pi \times 10^{6} t  \right) 

  vd=3.0 + 0.1 \times sin\left( 2\pi \times 10^{6} t  \right)


The $Solvetimestep2D setting in GUI interface is here
1. Press Time Dependent module, check the box and press Add new sweep modes.
2. Fill in the fields as needed!
2D Solvetimestep2D fig1.jpg
2D Solvetimestep2D fig2.jpg


related:
$savetimestep2D

取自 "http://yrwu-wk.ee.ntu.edu.tw/mediawiki/index.php?title=Solvetimestep2D&oldid=4284"