「$Withionmove」:修訂間差異
無編輯摘要 |
無編輯摘要 |
||
| 第70行: | 第70行: | ||
<math> D_{M} = \mu k_{B} T / q</math> | <math> D_{M} = \mu k_{B} T / q</math> | ||
The initial ion density is provided by traps in the steady state calculation. | The initial ion density is provided by traps in the steady state calculation. | ||
<br>'''<big><big>The $Withionmove setting in GUI interface is here</big></big>''' <br> | |||
1. After setting up the general structure, press '''Additional Functions'''.<br> | |||
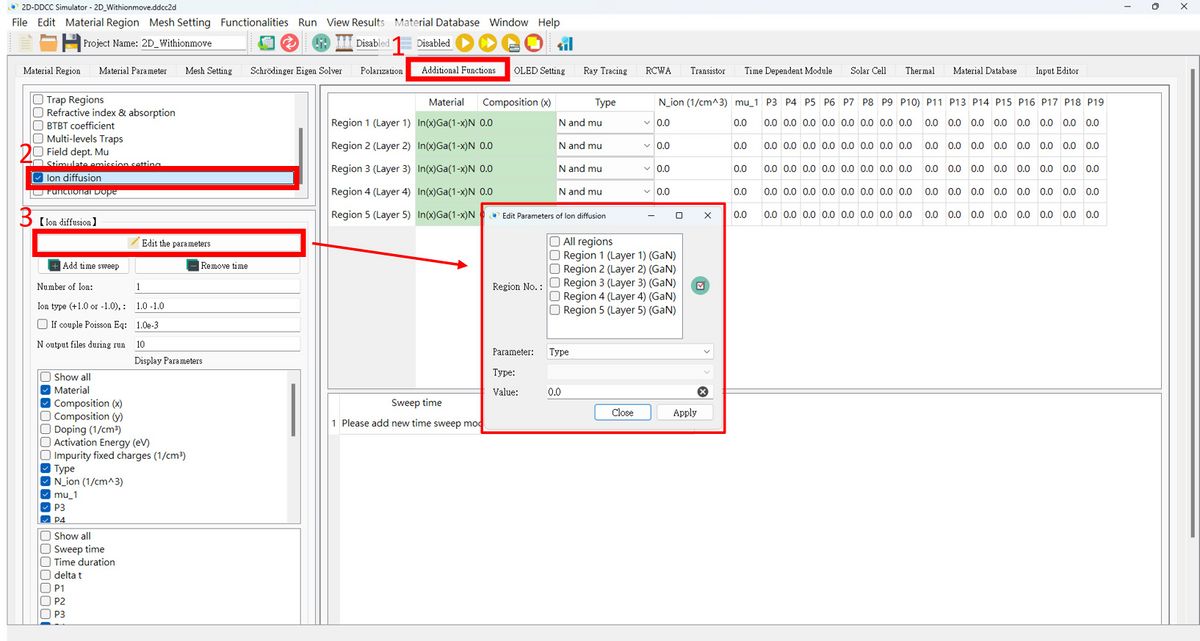
2. Check the box for '''Ion diffusion''' and press it to load the setting fields.<br> | |||
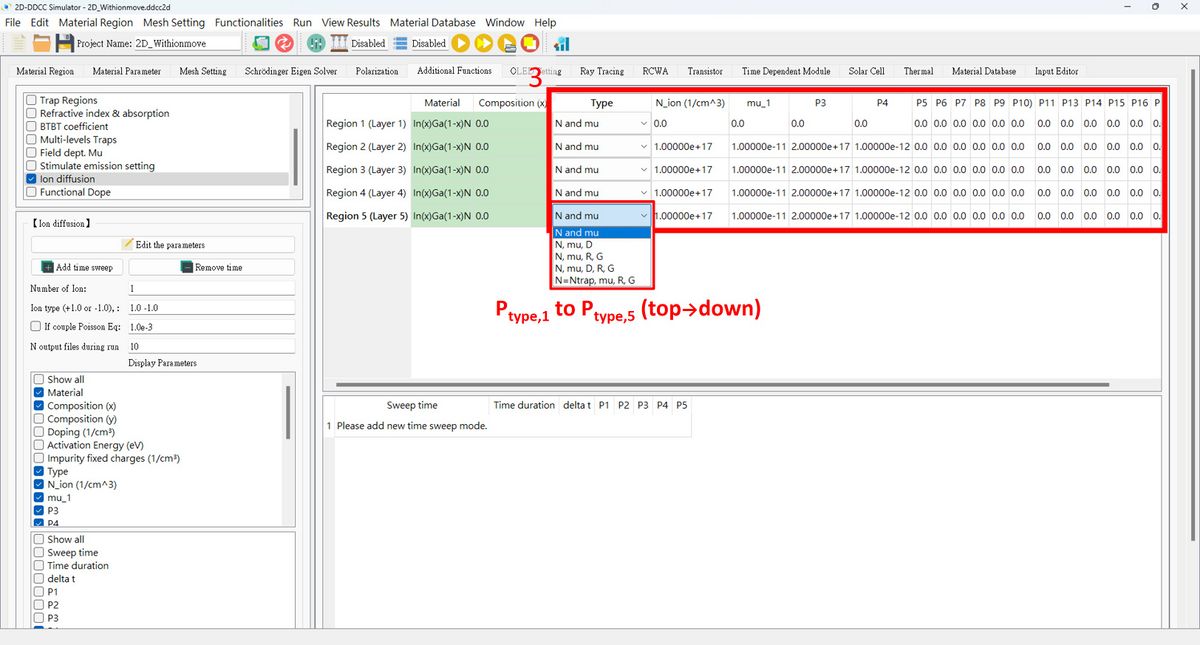
3. Press '''Edit the parameters''' and enter the value for each region, or we can input them directly in the fields on the right. There are 5 parameter types.<br> | |||
[[檔案:2D_Withionmove_fig1.jpg|1200px]]<br><br> | |||
[[檔案:2D_Withionmove_fig2.jpg|1200px]]<br><br> | |||
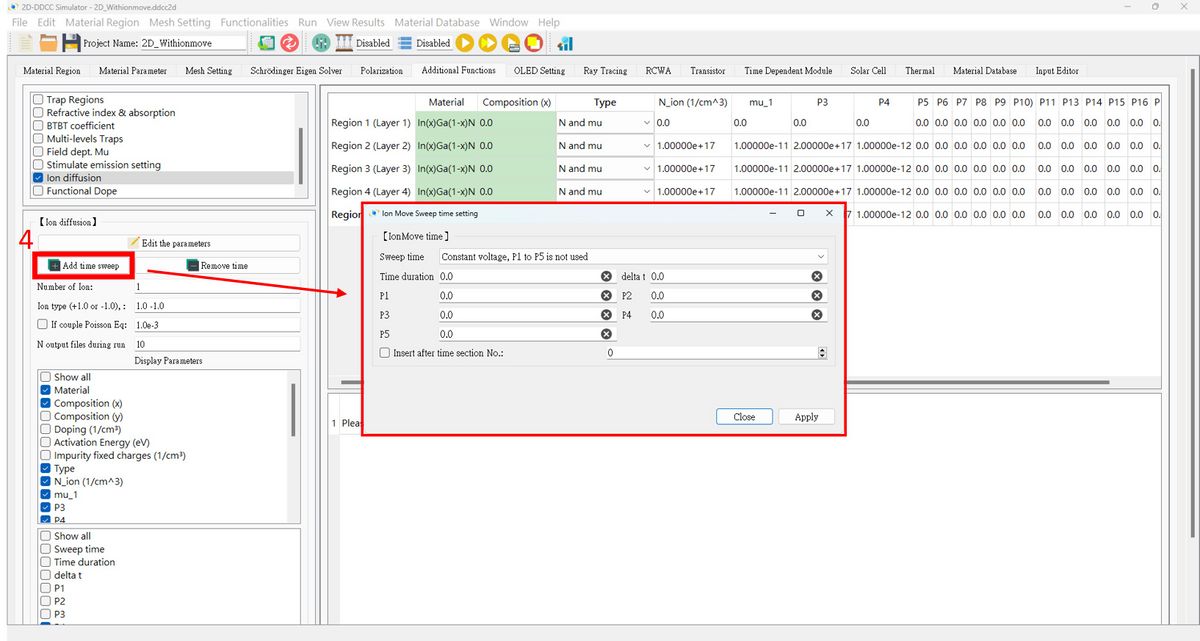
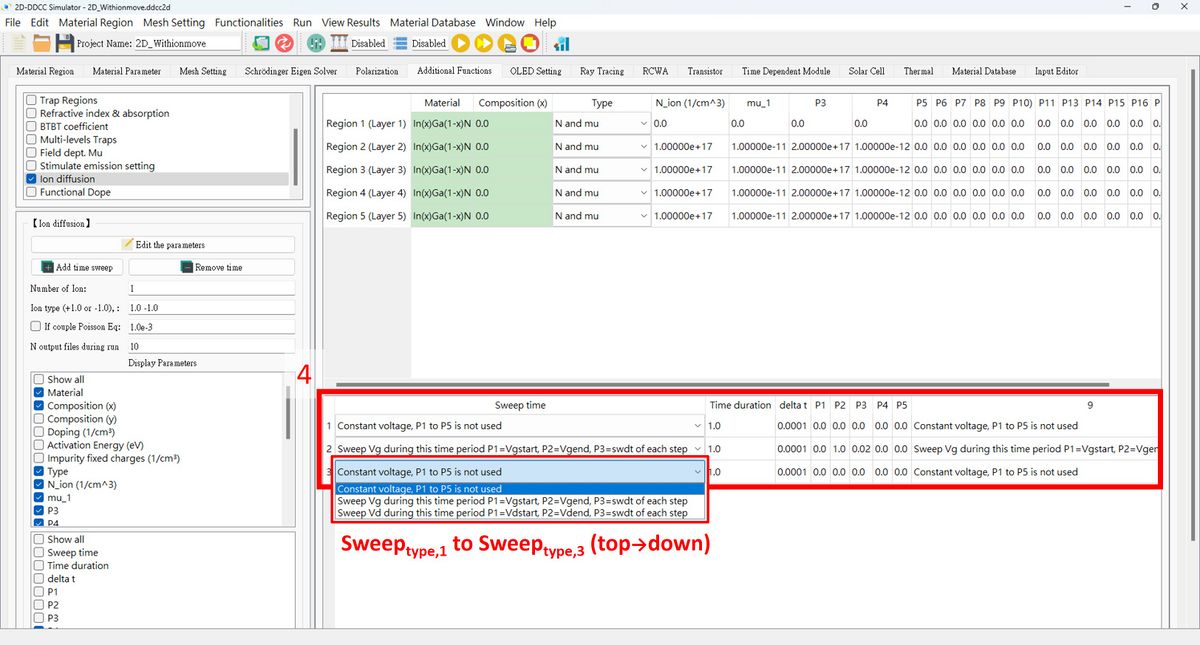
4. Press '''Add time sweep''' and fill in the fields for related setting. There are 3 Sweep time types.<br> | |||
[[檔案:2D_Withionmove_fig3.jpg|1200px]]<br><br> | |||
[[檔案:2D_Withionmove_fig4.jpg|1200px]]<br><br> | |||
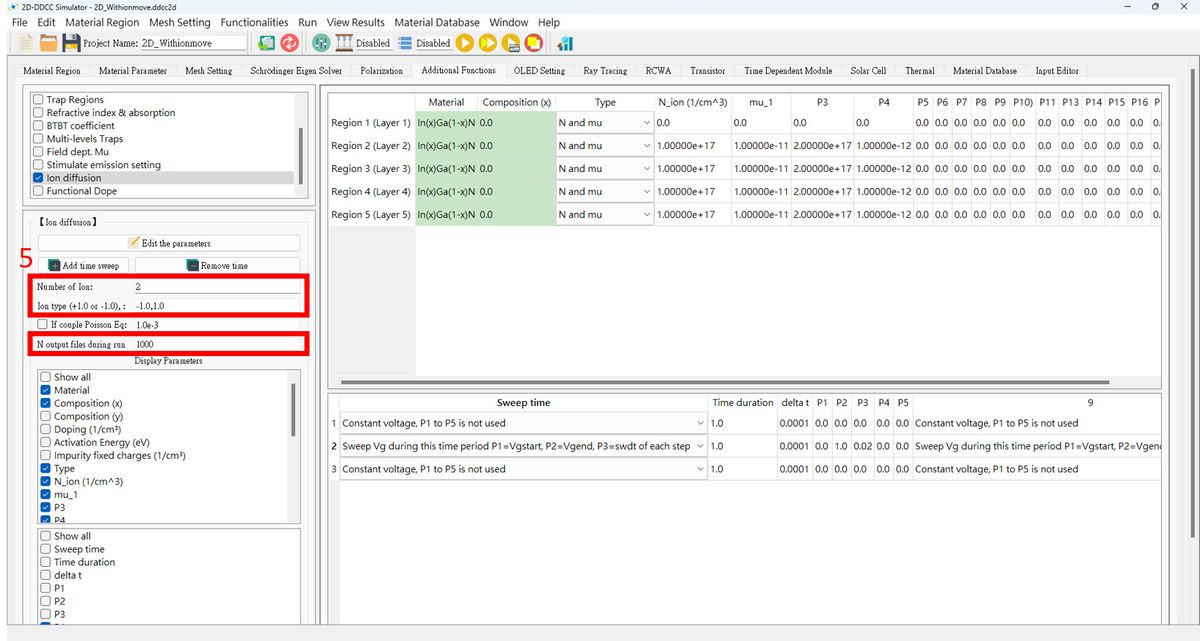
5. Fill in these fields as needed!<br> | |||
[[檔案:2D_Withionmove_fig5.jpg|1200px]]<br><br> | |||
See related commands <br> | See related commands <br> | ||
Related commands: [[$Withionmove]] [[$IonMovewithPoisson]] [[*.time_ion]] | Related commands: [[$Withionmove]] [[$IonMovewithPoisson]] [[*.time_ion]] | ||
於 2024年12月26日 (四) 09:57 的最新修訂
When the system has ion to perform as drift-diffusion equations, we solve the time dependent drift-diffusion for slow ion move simulation. Since the ion moves may not be governed fermi-level concept. We simply treat is a tradiational drift-diffusion equations.
Ideally, the ion density is given by initial setting. The total ion number should be fixed. The program is aim to model multi-ions drift-diffusion. The command is as following.
$Withionmove
Sweep_type_1 P1 P2 P3 P4 P5 ...
Sweep_type_1 P1 P2 P3 P4 P5 ..
...
...
Sweep_type_N_{sweep P1 P2 P3 P4 P5 ..
p3 p4 Parameters of the 1 layer
p3 p4 Parameters of the 2 layer
p3 p4 Parameters of the 3 layer
....
.....
p3 p4 Parameters of the $totalregion layer
: The number of runs for the time step : The number of output results for each run Sweep_type: 1: constant voltage, P1 to P5 is not used 2: Sweep Vg during this time period P1=Vgstart, P2=Vgend, P3=swdt of each step (step Number= 3: Sweep Vd during this time period P1=Vdstart, P2=Vdend, P3=swdt of each step 4,5,6.... leave for future use : The time for the first run. The time for the 2nd run. is the for each sweep. How many ions are considered. If we only want to consider 1 negative ion,we can put 1 The sign of ions. only accept
For example: Consider 2 ions, 1st is negative charges, 2nd is positive charges, total 5 Regions we can
$Withionmove 3 1000 1 1.00 1.0d-4 3 1.00 1.0d-4 0.0 1.0 0.02 1 1.00 1.0d-4 2 -1.0 1.0 1 0.0e17 0.0 0.0e17 0.0 1 1.0e17 1.0e-11 2.0e17 1.0e-12 1 1.0e17 1.0e-11 2.0e17 1.0e-12 1 1.0e17 1.0e-11 2.0e17 1.0e-12 1 1.0e17 1.0e-11 2.0e17 1.0e-12
is the parameter type: it depends on ion number 1: , ,........ 2: , ,........ 3: , ,........ 4: , ,........ 5: , ,........
When type 1 is chosen, we only put mobility , and the diffusion coefficient is calculated with Einstein relation, where
When type 2 is chosen, the diffusion coefficient is given by input For type==3, the ion mobility, quench term for R, Generation term for G is provided. For type==4, the ion mobility, diffusion coefficients, quench term for R, Generation term for G is provided.
For type==5, the ion mobility, quench term for R, Generation term for G is provided. The initial ion density is provided by traps in the steady state calculation.
The $Withionmove setting in GUI interface is here
1. After setting up the general structure, press Additional Functions.
2. Check the box for Ion diffusion and press it to load the setting fields.
3. Press Edit the parameters and enter the value for each region, or we can input them directly in the fields on the right. There are 5 parameter types.
4. Press Add time sweep and fill in the fields for related setting. There are 3 Sweep time types.
5. Fill in these fields as needed!
See related commands
Related commands: $Withionmove $IonMovewithPoisson *.time_ion