"$outputwave" 修訂間的差異
| 行 1: | 行 1: | ||
| − | 2D-DDCC solves the Poisson Drift-diffusion self-consistently. If we want to solve Schrodiner equations and get the eigen values, it would be very time consuming. Therefore, there is a special function to get the only 1D eigen wave functions and 1D eigen levels in the cross section when Poisson and drift-diffusion solver is solved. Using [[$outputwave]] can achieve this. When this command is used, the program will find top contact's type equal to 2, 21, 22, 7 to solve the problem. Actually this program is |
+ | 2D-DDCC solves the Poisson Drift-diffusion self-consistently. If we want to solve Schrodiner equations and get the eigen values, it would be very time consuming. Therefore, there is a special function to get the only 1D eigen wave functions and 1D eigen levels in the cross section when Poisson and drift-diffusion solver is solved. Using [[$outputwave]] can achieve this. When this command is used, the program will find top contact's type equal to 2, 21, 22, 7, and 3(newly added) to solve the problem. Actually this program is designed for HEMT or MOSFET devices. (But now it is expanded to LED problem). It will solve the electron, heavy hole and light hole's eigen value and eigen functions. If Epp, nr, and sigma is assigned, it will output the PL result. The format is |
$useschrodn |
$useschrodn |
||
| 行 5: | 行 5: | ||
Although 2D solver is based on FEM, when the cross section solver is called, the program solve this problem using FD scheme. Therefore, we need to |
Although 2D solver is based on FEM, when the cross section solver is called, the program solve this problem using FD scheme. Therefore, we need to |
||
| − | define Y_top and Y_depth as we used in 1D-DDCC Schrodinger solver to solve this problem. We also need to set N_grid to decide the dy in the FD Schrodinger solver solver. Y_int is for solver to know where is oxide insulator and semiconductor interface. However, this input is no longer used. Therefore, the user can put any value, which will not affect the output. <br> |
+ | define Y_top and Y_depth as we used in 1D-DDCC Schrodinger solver to solve this problem. We also need to set N_grid to decide the dy in the FD Schrodinger solver solver. Y_int is for solver to know where is oxide insulator and semiconductor interface. However, this input is no longer used. Therefore, the user can put any value between Y_top and Y_depth, which will not affect the output. <br> |
| − | <br> Note that this command is similar to [[$useschrodn]]. The difference is that [[$useschrodn]] will solve Poisson+1D |
+ | <br> Note that this command is similar to [[$useschrodn]]. The difference is that [[$useschrodn]] will solve Poisson+1D Schrondinger (all sections) self-consistently. And [[$useschrodn]] will only calculate electron. |
| + | [[$outputwave]] will only output wave function at the end of each bias converged. The related output file would be |
||
| + | |||
| + | Project_xxx*.1dEihh ! 1D section's heavy hole eigen values |
||
| + | Project_xxx*.1dEilh ! 1D section's light hole eigen values |
||
| + | Project_xxx*.1dEin ! 1D section's electron eigen values |
||
| + | Project_xxx*.1dinfo ! some information in simulation |
||
| + | Project_xxx*.1doverlap ! electron and heavy hole overlap |
||
| + | Project_xxx*.1doverlaplh ! electron and light hole overlap |
||
| + | Project_xxx*.1dPL ! total PL and each cross section's PL |
||
| + | Project_xxx*.1dschn ! estimate electron density from Schrodinger solver with average electron Fermi level |
||
| + | Project_xxx*.1dschp ! estimate hole density from Schrodinger solver with average electron Fermi level |
||
| + | Project_xxx*.1dwv ! 1D section's electron eigen functions |
||
| + | Project_xxx*.1dwvhh ! 1D section's heavy hole eigen functions |
||
| + | Project_xxx*.1dwvlh ! 1D section's light hole eigen functions |
||
於 2017年12月13日 (三) 20:34 的修訂
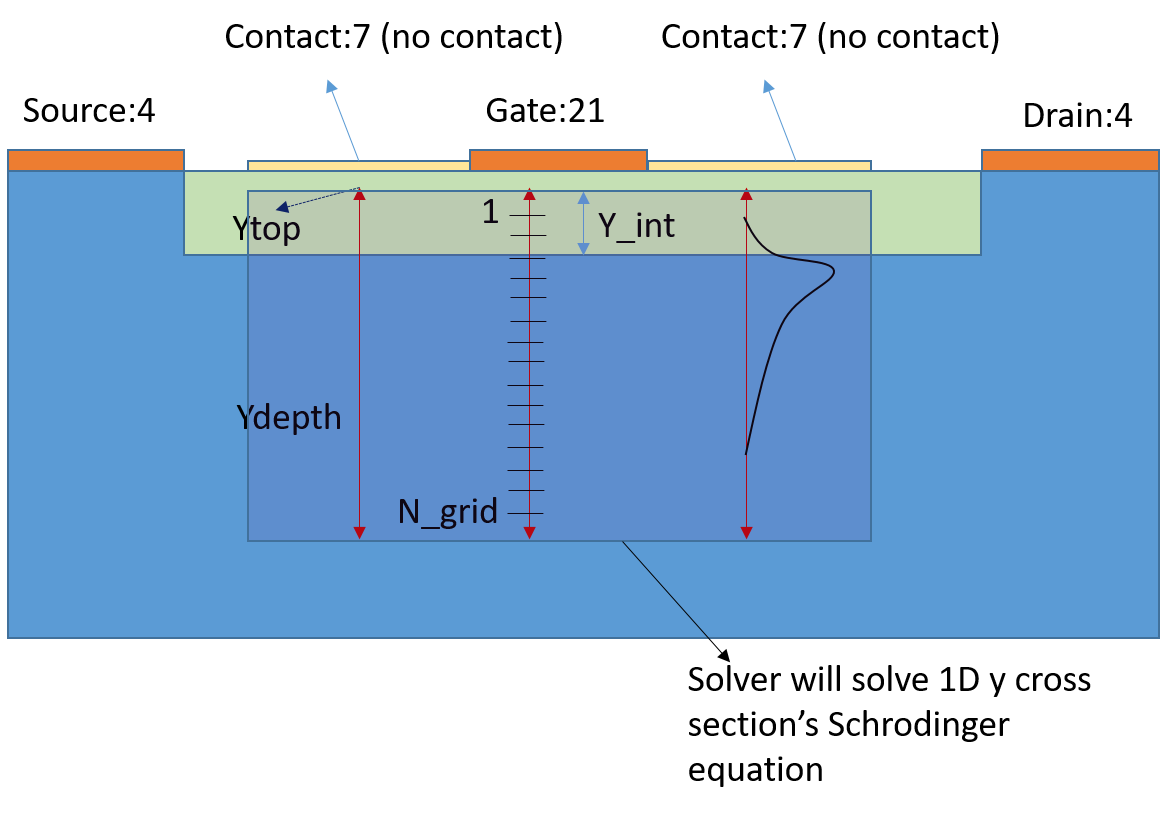
2D-DDCC solves the Poisson Drift-diffusion self-consistently. If we want to solve Schrodiner equations and get the eigen values, it would be very time consuming. Therefore, there is a special function to get the only 1D eigen wave functions and 1D eigen levels in the cross section when Poisson and drift-diffusion solver is solved. Using $outputwave can achieve this. When this command is used, the program will find top contact's type equal to 2, 21, 22, 7, and 3(newly added) to solve the problem. Actually this program is designed for HEMT or MOSFET devices. (But now it is expanded to LED problem). It will solve the electron, heavy hole and light hole's eigen value and eigen functions. If Epp, nr, and sigma is assigned, it will output the PL result. The format is
$useschrodn N_grid Y_top Y_depth Y_interface(Y_int)
Although 2D solver is based on FEM, when the cross section solver is called, the program solve this problem using FD scheme. Therefore, we need to
define Y_top and Y_depth as we used in 1D-DDCC Schrodinger solver to solve this problem. We also need to set N_grid to decide the dy in the FD Schrodinger solver solver. Y_int is for solver to know where is oxide insulator and semiconductor interface. However, this input is no longer used. Therefore, the user can put any value between Y_top and Y_depth, which will not affect the output.
Note that this command is similar to $useschrodn. The difference is that $useschrodn will solve Poisson+1D Schrondinger (all sections) self-consistently. And $useschrodn will only calculate electron.
$outputwave will only output wave function at the end of each bias converged. The related output file would be
Project_xxx*.1dEihh ! 1D section's heavy hole eigen values Project_xxx*.1dEilh ! 1D section's light hole eigen values Project_xxx*.1dEin ! 1D section's electron eigen values Project_xxx*.1dinfo ! some information in simulation Project_xxx*.1doverlap ! electron and heavy hole overlap Project_xxx*.1doverlaplh ! electron and light hole overlap Project_xxx*.1dPL ! total PL and each cross section's PL Project_xxx*.1dschn ! estimate electron density from Schrodinger solver with average electron Fermi level Project_xxx*.1dschp ! estimate hole density from Schrodinger solver with average electron Fermi level Project_xxx*.1dwv ! 1D section's electron eigen functions Project_xxx*.1dwvhh ! 1D section's heavy hole eigen functions Project_xxx*.1dwvlh ! 1D section's light hole eigen functions