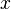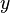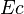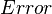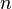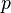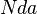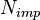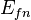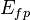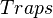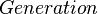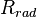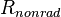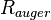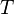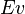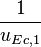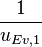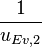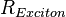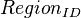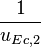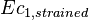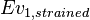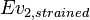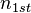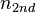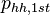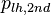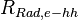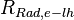"*.fet" 修訂間的差異
出自 DDCC TCAD TOOL Manual
| (未顯示同一使用者於中間所作的 10 次修訂) | |||
| 行 7： | 行 7： | ||
new updated version (since 2023) |
new updated version (since 2023) |
||
| − | <math> x</math> <math> y</math> <math> Ec</math> <math> Error</math> <math> n</math> <math> p </math> <math>Nda</math> <math> N_{imp}</math> <math> E_{fn}</math> <math> E_{fp} </math> <math>Traps</math> <math> Generation </math> <math>R_{rad}</math> <math>R_{nonrad}</math> <math>R_{auger}</math> <math> T</math> <math>Ev </math> <math>\frac{1}{u_{Ec,1}}</math> <math>\frac{1}{u_{Ev,1}}</math> <math>\frac{1}{u_{Ev,2}}</math> <math> R_{Exciton}</math> <math> |
+ | <math> x</math> <math> y</math> <math> Ec</math> <math> Error</math> <math> n</math> <math> p </math> <math>Nda</math> <math> N_{imp}</math> <math> E_{fn}</math> <math> E_{fp} </math> <math>Traps</math> <math> Generation </math> <math>R_{rad}</math> <math>R_{nonrad}</math> <math>R_{auger}</math> <math> T</math> <math>Ev </math> <math>\frac{1}{u_{Ec,1}}</math> <math>\frac{1}{u_{Ev,1}}</math> <math>\frac{1}{u_{Ev,2}}</math> <math> R_{Exciton}</math> <math>Region_{ID} </math> <math>\frac{1}{u_{Ec,2}}</math> <math>Ec_{1,strained}</math> <math>Ec_{2,strained}</math> <math>Ev_{1,strained}</math> <math>Ev_{2,strained}</math> <math>n_{1st}</math> <math>n_{2nd}</math> <math>p_{hh,1st}</math> <math>p_{lh,2nd}</math> <math>R_{Rad,e-hh}</math> <math>R_{Rad,e-lh}</math> |
| + | |||
| + | |||
| + | new updated version (since 2024.04) |
||
| + | |||
| + | <math> x</math> <math> y</math> <math> Ec</math> <math> Error</math> <math> n</math> <math> p </math> <math>Nda</math> <math> N_{imp}</math> <math> E_{fn}</math> <math> E_{fp} </math> <math>Traps</math> <math> Generation </math> <math>R_{rad}</math> <math>R_{nonrad}</math> <math>R_{auger}</math> <math> T</math> <math>Ev </math> <math>\frac{1}{u_{Ec,1}}</math> <math>\frac{1}{u_{Ev,1}}</math> <math>\frac{1}{u_{Ev,2}}</math> <math> R_{Exciton}</math> <math>Region_{ID} </math> <math>\frac{1}{u_{Ec,2}}</math> <math>Ec_{1,strained}</math> <math>Ec_{2,strained}</math> <math>Ev_{1,strained}</math> <math>Ev_{2,strained}</math> <math>n_{1st}</math> <math>n_{2nd}</math> <math>p_{hh,1st}</math> <math>p_{lh,2nd}</math> <math>R_{Rad,e-hh}</math> <math>R_{Rad,e-lh}</math> <math>\int^{y_T}_{y_B} Jn_{x} dy</math> <math>\int^{x_R}_{x_L} Jn_{y} dx</math> <math>\int^{y_T}_{y_B} Jp_{x} dy</math> <math>\int^{x_R}_{x_L} Jp_{y} dx</math> |
||
| + | |||
| + | <math>\int^{y_T}_{y_B} Jn_{x} dy</math> Mean in each node point, the current flow in the x direction through at point is the integration from bottom neighbor point to the top neighbor point. The integration has a weighting of current from 0 (neighbor point) to 1 (node point) with FEM algorithm. |
||
| + | |||
| + | <math>\int^{x_R}_{x_L} Jn_{y} dx</math> Mean in each node point, the current flow in the y direction through at point is the integration from left neighbor point to the right neighbor point. The integration has a weighting of current from 0 (neighbor point) to 1 (node point) with FEM algorithm. <br> |
||
| + | '''Note:''' This is a integrated current density, not the current density. So it might have a larger current if the neighbor point is far away since the integration distance is longer. |
||
於 2024年4月7日 (日) 16:42 的最新修訂
Format Old format for earlier version
x y Ec Error n p Nda Impurity Efn Efp Traps generation Radiative non-radiative Auger temperature Ev uofEc uofEv uofEv2 Exciton region_num
new updated version (since 2023)
new updated version (since 2024.04)
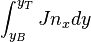Mean in each node point, the current flow in the x direction through at point is the integration from bottom neighbor point to the top neighbor point. The integration has a weighting of current from 0 (neighbor point) to 1 (node point) with FEM algorithm.
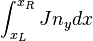Mean in each node point, the current flow in the y direction through at point is the integration from left neighbor point to the right neighbor point. The integration has a weighting of current from 0 (neighbor point) to 1 (node point) with FEM algorithm.
Note: This is a integrated current density, not the current density. So it might have a larger current if the neighbor point is far away since the integration distance is longer.
