"*.vg *-pl.info" 修訂間的差異
出自 DDCC TCAD TOOL Manual
| 行 15： | 行 15： | ||
For n=1,C_e_N |
For n=1,C_e_N |
||
for m=1,V_HH_M |
for m=1,V_HH_M |
||
| − | for |
+ | for E_{\hbar\omega}=0, Emax |
| − | for Ek = <math>Ei - 5\sigma , Ei+5\sigma </math> |
+ | for Ek = <math>Ei - 5\sigma , Ei+5\sigma </math> |
| − | <math> |
+ | <math> If Ek > E_{n,e}-E_{hh,m} then |
| + | fe = \frac{1}{1+exp(\frac{Ek-Efn}{k_BT})} </math> |
||
<math> fh = \frac{1}{1+exp(\frac{Efp-Ek}{k_BT})} </math> |
<math> fh = \frac{1}{1+exp(\frac{Efp-Ek}{k_BT})} </math> |
||
<math> Rsp(Ei) = Rsp(Ei) + dE * Ei * |\langle\phi_{e,n} |\phi_{hh,m} \rangle |^2 * fe * fh* \frac{1}{\sqrt{2\pi} \sigma} exp( -\frac{(Ek-Ei)^2}{2*\sigma^2}) </math> |
<math> Rsp(Ei) = Rsp(Ei) + dE * Ei * |\langle\phi_{e,n} |\phi_{hh,m} \rangle |^2 * fe * fh* \frac{1}{\sqrt{2\pi} \sigma} exp( -\frac{(Ek-Ei)^2}{2*\sigma^2}) </math> |
||
於 2025年1月28日 (二) 15:59 的修訂
C_e_N, V_HH_M, V_LH_L, nr , Epp
For n=1,C_e_N
for m=1,V_HH_M
end
end
For n=1,C_e_N
for m=1,V_LH_L
end
end
The PL of e to HH can be calculated by
Rsp=0.0
For n=1,C_e_N
for m=1,V_HH_M
for E_{\hbar\omega}=0, Emax
for Ek =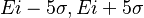 
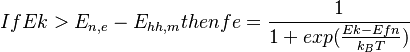
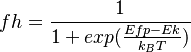
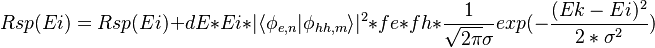end
end
end
end
The PL of e to LH can be calculated by
Rsp=0.0
For n=1,C_e_N
for m=1,V_LH_:
for Ei=0, Emax
for Ek = Ei - 5\sigma , Ei+5\sigma
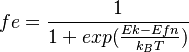
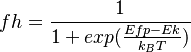
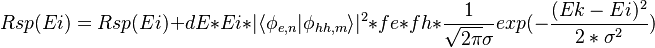end
end
end
end
