$ifapplyEgofT

Since the DDCC has the capability of solving the Poisson, drift-diffusion, and thermal solver self-consistently. It will need to consider the possibility of bandgap narrowing with temperature. Therefore, we can apply the temperature-dependent coefficients for the material's bandgap. Usually, the temperature-dependent bandgap can be expressed as:

 $Eg(T) = Eg(0) - \frac{\gamma \times T^{2} }{ T + \beta}$

In the program, we don't set Eg(0), instead, we set Eg(300)

 $Eg(T) = Eg(300) + \frac{\gamma \times 300^{2} }{ 300 + \beta}  - \frac{\gamma \times T^{2} }{ T + \beta}$

Therefore, to enable the temperature-dependent Eg in the simulation, we need to add
.

$ifapplyEgofT
$Eg(300)_{1}$  $\gamma$  $\beta$
$Eg(300)_{2}$  $\gamma$  $\beta$
$Eg(300)_{3}$  $\gamma$  $\beta$
$Eg(300)_{4}$  $\gamma$  $\beta$
...
...
to layer N

If some material's coefficient cannot be found, please make $\gamma = 0$. So the program will keep the bandgap of this region as constant.
Note that

Eg(300) is the Eg at 300K. With this modified equation, we can make the Eg is always the same as the original Eg at 300K

For advanced users who use libmodpar.f90. This function may have a problem if the bandgap is changed in libmodpar.f90

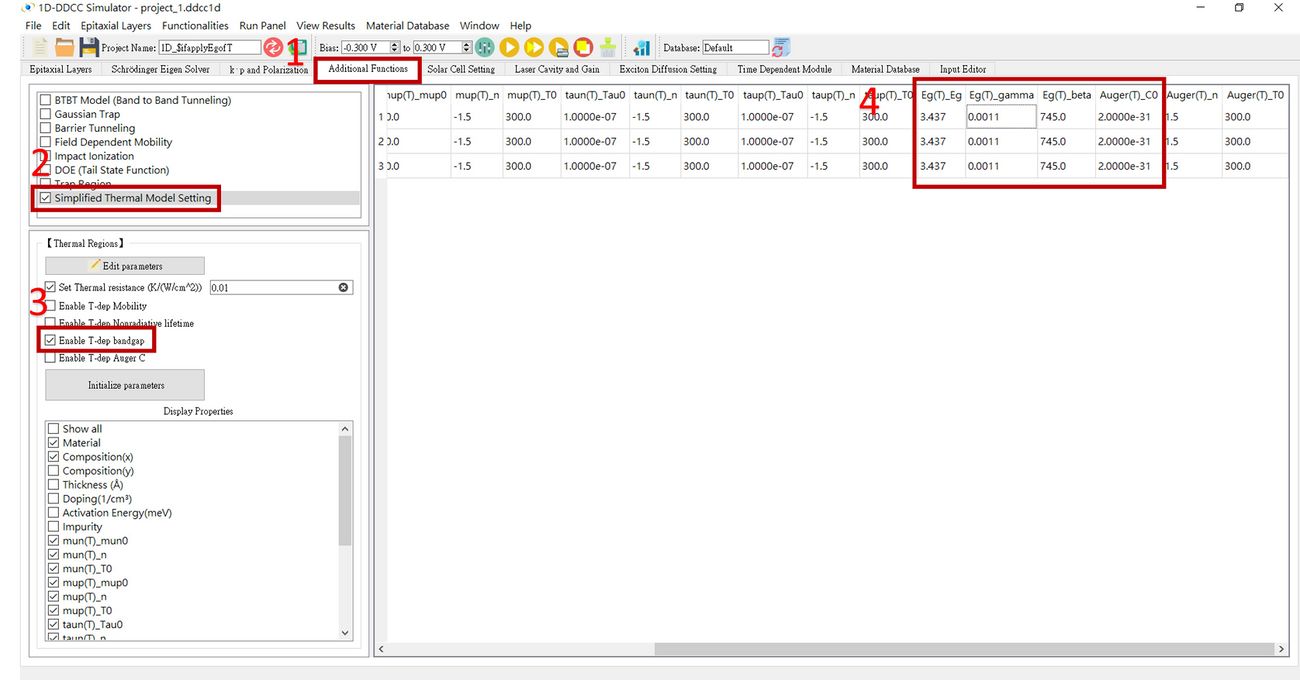
The $ifapplyEgofT setting for 1D-DDCC in GUI interface

The parameters are modified in Step 4.

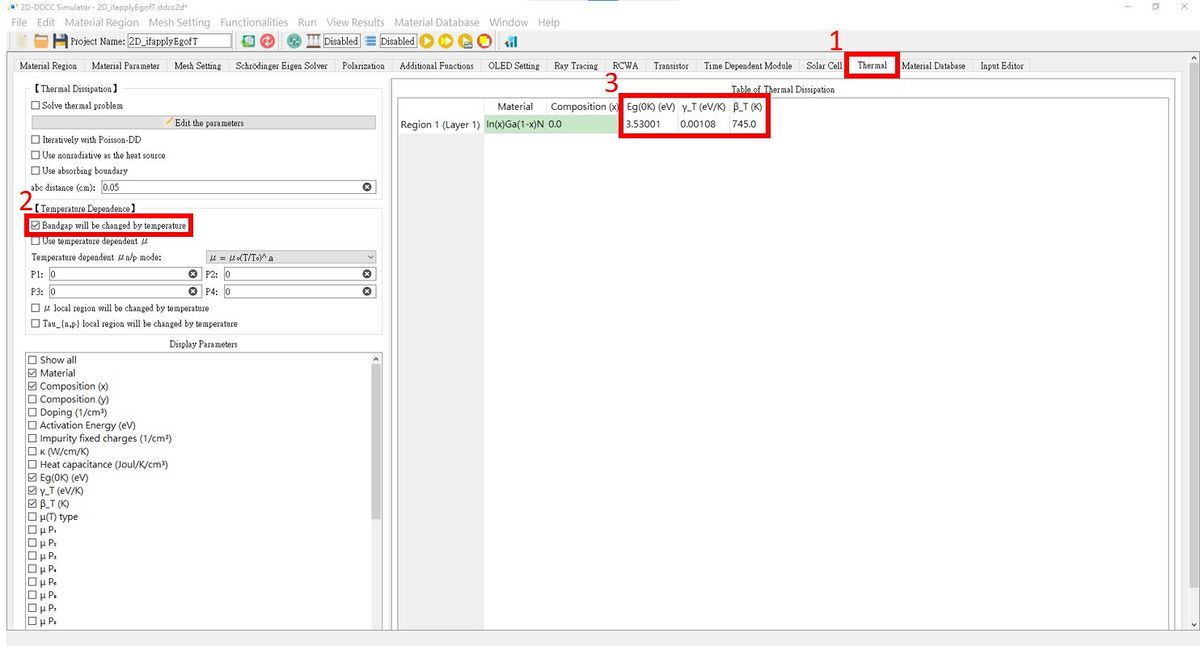
The $ifapplyEgofT setting for 2D-DDCC in GUI interface
Press Thermal, check the box and set the fields as needed!

The related commands are: $ifapplytauofT, $ifapplymuofT, $ifapplyEgofT, $ifTversusJ