$usemunpfunc

Function for organic material. We usually assume the carrier mobility is depend on electrical field and follow Poole-Frenkel field dependent mobility equation.

Mobility follow this equation

$\mu=\mu_0 exp(\beta\sqrt{E})$

Where　

• $\mu_0$ is the zero-field mobility
• $\beta$ is the factor of mobility increasing
• $E$ is the electric field.

Format

$usemunpfunc
1 μe βe μh βh

Parameter Explanation

$\mu_n=\mu_0 exp(\beta\sqrt{E})$,  $\mu_p=\mu_0 exp(\beta\sqrt{E})$ 

• μe : electron zero-field mobility. $(cm^{2}eV^{-1}s^{-1})$
• βe : electron beta. $(eV^{-1/2})$
• μh : hole zero-field mobility. $(cm^{2}eV^{-1}s^{-1})$
• βh : hole beta. $(eV^{-1/2})$

$usemunpfunc
11 μe βe μh βh $v_{n,sat}$ $v_{p,sat}$

Parameter Explanation

• μe : electron zero-field mobility. $(cm^{2}eV^{-1}s^{-1})$
• βe : electron beta. $(eV^{-1/2})$
• μh : hole zero-field mobility. $(cm^{2}eV^{-1}s^{-1})$
• βh : hole beta. $(eV^{-1/2})$
• $v_{n,sat}$ saturate electron velocity (cm/s)
• $v_{p,sat}$ saturate hole velocity (cm/s)

 $\mu_{n,temp}=\mu_0 exp(\beta\sqrt{E})$,  $\mu_{p,temp}=\mu_0 exp(\beta\sqrt{E})$ 

 If $\mu_{n,temp} \times E > v_{n,sat}, then \mu_n = \frac{v_{n,sat}}{E}$
 If $\mu_{p,temp} \times E > v_{p,sat}, then \mu_p = \frac{v_{p,sat}}{E}$

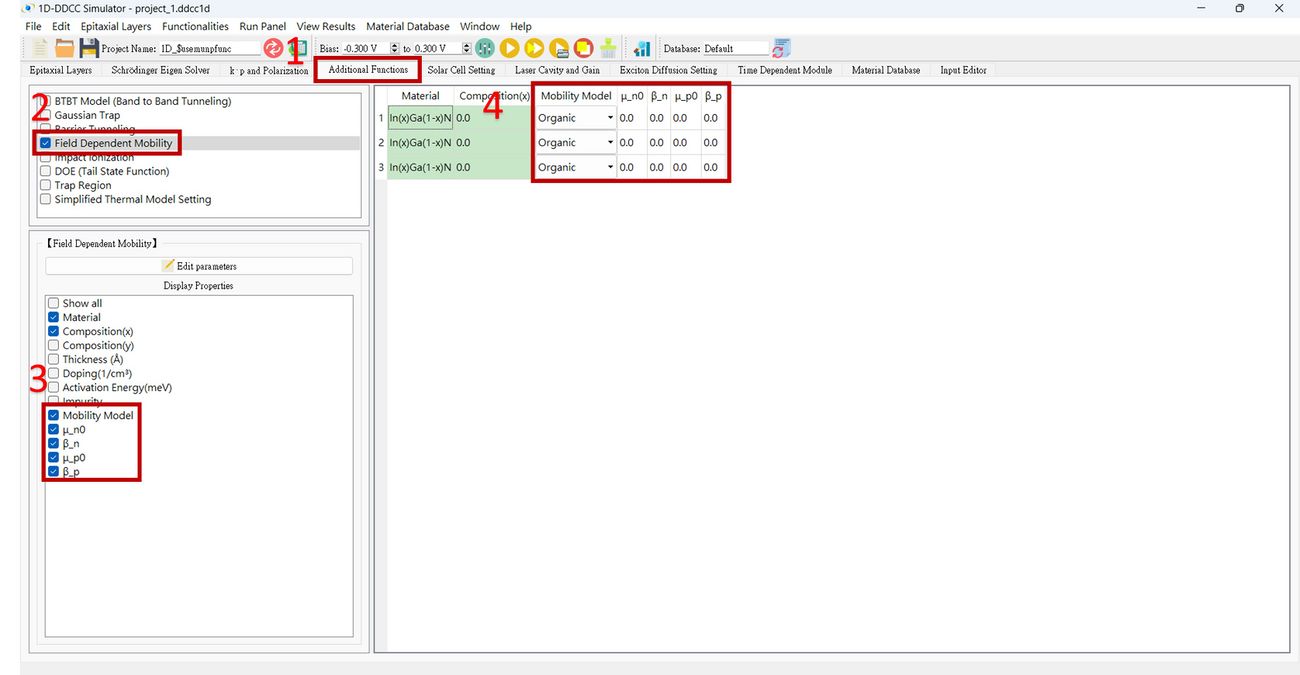
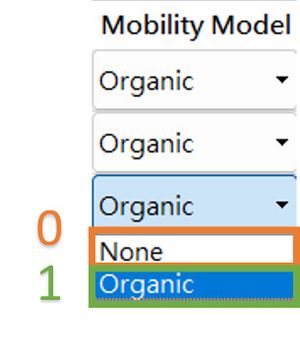
The $usemunpfunc setting for 1D-DDCC in GUI interface

The parameters are modified in step 4.