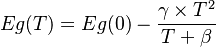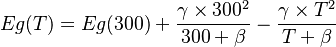"$ifapplyEgofT" 修訂間的差異
| (未顯示由 1 位使用者於中間所作的 2 次修訂) | |||
| 行 1: | 行 1: | ||
| − | Since the DDCC has the capability of solving the Poisson, drift-diffusion, and thermal solver self-consistently. It will need to consider the possibility of bandgap narrowing with temperature. Therefore, we can apply the temperature |
+ | Since the DDCC has the capability of solving the Poisson, drift-diffusion, and thermal solver self-consistently. It will need to consider the possibility of bandgap narrowing with temperature. Therefore, we can apply the temperature-dependent coefficients for the material's bandgap. Usually, the temperature-dependent bandgap can be expressed as: <br> |
<math> Eg(T) = Eg(0) - \frac{\gamma \times T^{2} }{ T + \beta} </math> |
<math> Eg(T) = Eg(0) - \frac{\gamma \times T^{2} }{ T + \beta} </math> |
||
| ⚫ | |||
| + | In the program, we don't set Eg(0), instead, we set Eg(300) |
||
| + | |||
| + | <math> Eg(T) = Eg(300) + \frac{\gamma \times 300^{2} }{ 300 + \beta} - \frac{\gamma \times T^{2} }{ T + \beta} </math> |
||
| + | |||
| ⚫ | |||
$ifapplyEgofT |
$ifapplyEgofT |
||
| − | <math>Eg( |
+ | <math>Eg(300)_{1} </math> <math> \gamma </math> <math> \beta </math> |
| − | <math>Eg( |
+ | <math>Eg(300)_{2} </math> <math> \gamma </math> <math> \beta </math> |
| − | <math>Eg( |
+ | <math>Eg(300)_{3} </math> <math> \gamma </math> <math> \beta </math> |
| − | <math>Eg( |
+ | <math>Eg(300)_{4} </math> <math> \gamma </math> <math> \beta </math> |
... |
... |
||
... |
... |
||
| 行 16: | 行 20: | ||
If some material's coefficient cannot be found, please make <math> \gamma = 0 </math>. So the program will keep the bandgap of this region as constant. <br> |
If some material's coefficient cannot be found, please make <math> \gamma = 0 </math>. So the program will keep the bandgap of this region as constant. <br> |
||
Note that <br> |
Note that <br> |
||
| − | Eg( |
+ | Eg(300) is the Eg at 300K. With this modified equation, we can make the Eg is always the same as the original Eg at 300K |
| − | <math> Eg(300) = Eg(0) - \frac{\gamma \times 300^{2} }{ 300 + \beta} </math> may not be the same as the Eg in the [[$parameters]]. Please be careful to use this command. |
||
<br><br> |
<br><br> |
||
| − | For advanced users who use libmodpar.f90. This function may have problem if the bandgap is changed in libmodpar.f90 |
+ | For advanced users who use libmodpar.f90. This function may have a problem if the bandgap is changed in libmodpar.f90 |
| + | |||
| + | |||
| + | <br>'''<big><big>The $ifapplyEgofT setting in GUI interface is here</big></big>''' <br> |
||
| + | Press '''Thermal''', check the box and set the fields as needed!<br> |
||
| + | [[檔案:2D_ifapplyEgofT_fig1.jpg|1200px]]<br><br> |
||
| + | |||
| + | |||
| + | The related commands are: [[$ifapplytauofT]], [[$ifapplymuofT]], [[$ifapplyEgofT]], [[$ifTversusJ]] |
||
於 2024年11月20日 (三) 19:35 的最新修訂
Since the DDCC has the capability of solving the Poisson, drift-diffusion, and thermal solver self-consistently. It will need to consider the possibility of bandgap narrowing with temperature. Therefore, we can apply the temperature-dependent coefficients for the material's bandgap. Usually, the temperature-dependent bandgap can be expressed as:
In the program, we don't set Eg(0), instead, we set Eg(300)
Therefore, to enable the temperature-dependent Eg in the simulation, we need to add
.
$ifapplyEgofT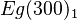
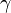
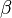
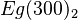
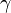
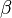
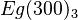
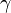
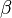
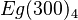
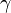
... ... to layer N
If some material's coefficient cannot be found, please make 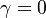 . So the program will keep the bandgap of this region as constant.
. So the program will keep the bandgap of this region as constant.
Note that
Eg(300) is the Eg at 300K. With this modified equation, we can make the Eg is always the same as the original Eg at 300K
For advanced users who use libmodpar.f90. This function may have a problem if the bandgap is changed in libmodpar.f90
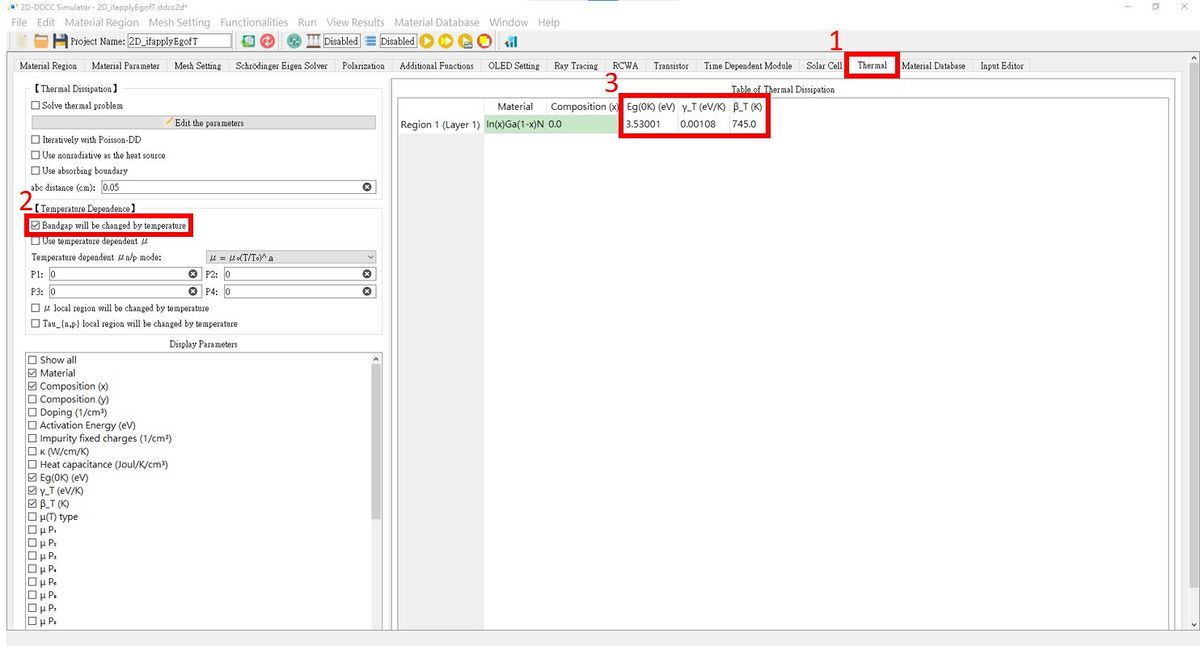
The $ifapplyEgofT setting in GUI interface is here
Press Thermal, check the box and set the fields as needed!
The related commands are: $ifapplytauofT, $ifapplymuofT, $ifapplyEgofT, $ifTversusJ