"$usemunpfunc" 修訂間的差異

出自 DDCC TCAD TOOL Manual
前往： 導覽、 搜尋
(已建立頁面，內容為 "Function for organic material. We usually assume the carrier mobility is depend on electrical field and follow Poole-Frenkel field dependent mobility equation. <bi...")
 
 
(未顯示由 2 位使用者於中間所作的 8 次修訂)
行 1： 行 1：
 
Function for organic material. We usually assume the carrier mobility is depend on electrical field and follow Poole-Frenkel field dependent mobility equation.
  
Function for organic material. We usually assume the carrier mobility is depend on electrical field and follow Poole-Frenkel field dependent mobility equation.
   
  +
Mobility follow this equation
   
⚫
<big><big>'''format'''</big></big>
 
  +
  +
<math>\mu=\mu_0 exp(\beta\sqrt{E})</math>
  +
  +
Where　
  +
* <math>\mu_0</math> is the zero-field mobility
  +
* <math>\beta</math> is the factor of mobility increasing
  +
* <math>E</math> is the electric field.
  +
  +
  +
  ⚫
<big><big>'''Format'''</big></big>
   
 
$usemunpfunc
  
$usemunpfunc
−
1 mue0 betae muh0 betah
  
  +
1 μe βe μh βh
  +
  +
  +
'''<big><big>Parameter Explanation</big></big>'''
  +
  +
<math>\mu_n=\mu_0 exp(\beta\sqrt{E})</math>, <math>\mu_p=\mu_0 exp(\beta\sqrt{E})</math>
  +
* μe : electron zero-field mobility. <math>(cm^{2}eV^{-1}s^{-1})</math>
  +
* βe : electron beta. <math>(eV^{-1/2})</math>
  +
* μh : hole zero-field mobility. <math>(cm^{2}eV^{-1}s^{-1})</math>
  +
* βh : hole beta. <math>(eV^{-1/2})</math>
  +
  +
  +
$usemunpfunc
  +
11 μe βe μh βh <math>v_{n,sat}</math> <math>v_{p,sat}</math>
  +
  +
  +
'''<big><big>Parameter Explanation</big></big>'''
  +
  +
  +
* μe : electron zero-field mobility. <math>(cm^{2}eV^{-1}s^{-1})</math>
  +
* βe : electron beta. <math>(eV^{-1/2})</math>
  +
* μh : hole zero-field mobility. <math>(cm^{2}eV^{-1}s^{-1})</math>
  +
* βh : hole beta. <math>(eV^{-1/2})</math>
  +
* <math>v_{n,sat}</math> saturate electron velocity (cm/s)
  +
* <math>v_{p,sat}</math> saturate hole velocity (cm/s)
  +
<math>\mu_{n,temp}=\mu_0 exp(\beta\sqrt{E})</math>, <math>\mu_{p,temp}=\mu_0 exp(\beta\sqrt{E})</math>
   
−
parameter explanation
  
  +
If <math> \mu_{n,temp} \times E > v_{n,sat}, then \mu_n = \frac{v_{n,sat}}{E} </math>
−
mue0 u8efbc9aelectron mobility at e 0 unit cm 2 ev -1 s -1
 
  +
If <math> \mu_{p,temp} \times E > v_{p,sat}, then \mu_p = \frac{v_{p,sat}}{E} </math>
−
betae u8efbc9aelectron beta unit ev -0.5
 
−
muh0 u8efbc9ahole mobility at e 0 unit cm 2 ev -1 s -1
 
−
betah u8efbc9ahole beta unit ev -0.5
  

於 2018年3月26日 (一) 10:21 的最新修訂

Function for organic material. We usually assume the carrier mobility is depend on electrical field and follow Poole-Frenkel field dependent mobility equation.

Mobility follow this equation


\mu=\mu_0 exp(\beta\sqrt{E})

Where　

  • \mu_0 is the zero-field mobility
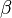  • \beta is the factor of mobility increasing
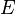  • E is the electric field.


Format 

$usemunpfunc
1 μe βe μh βh


Parameter Explanation 

\mu_n=\mu_0 exp(\beta\sqrt{E}),  \mu_p=\mu_0 exp(\beta\sqrt{E})
  • μe : electron zero-field mobility. (cm^{2}eV^{-1}s^{-1})
  • βe : electron beta. (eV^{-1/2})
  • μh : hole zero-field mobility. (cm^{2}eV^{-1}s^{-1})
  • βh : hole beta. (eV^{-1/2})


$usemunpfunc
11 μe βe μh βh v_{n,sat} v_{p,sat}


Parameter Explanation


  • μe : electron zero-field mobility. (cm^{2}eV^{-1}s^{-1})
  • βe : electron beta. (eV^{-1/2})
  • μh : hole zero-field mobility. (cm^{2}eV^{-1}s^{-1})
  • βh : hole beta. (eV^{-1/2})
  • v_{n,sat} saturate electron velocity (cm/s)
  • v_{p,sat} saturate hole velocity (cm/s)
 \mu_{n,temp}=\mu_0 exp(\beta\sqrt{E}),  \mu_{p,temp}=\mu_0 exp(\beta\sqrt{E}) 

 If  \mu_{n,temp} \times E > v_{n,sat}, then \mu_n = \frac{v_{n,sat}}{E} 
 If  \mu_{p,temp} \times E > v_{p,sat}, then \mu_p = \frac{v_{p,sat}}{E}
取自 "http://yrwu-wk.ee.ntu.edu.tw/mediawiki/index.php?title=$usemunpfunc&oldid=838"