「$usemunpfunc」:修訂間差異
跳至導覽
跳至搜尋
無編輯摘要 |
無編輯摘要 |
||
| (未顯示由 1 位使用者於中間所作的 6 次修訂) | |||
| 第29行: | 第29行: | ||
$usemunpfunc | $usemunpfunc | ||
11 μe βe μh βh <math> | 11 μe βe μh βh <math>v_{n,sat}</math> <math>v_{p,sat}</math> | ||
'''<big><big>Parameter Explanation</big></big>''' | '''<big><big>Parameter Explanation</big></big>''' | ||
* μe : electron zero-field mobility. <math>(cm^{2}eV^{-1}s^{-1})</math> | * μe : electron zero-field mobility. <math>(cm^{2}eV^{-1}s^{-1})</math> | ||
| 第39行: | 第39行: | ||
* μh : hole zero-field mobility. <math>(cm^{2}eV^{-1}s^{-1})</math> | * μh : hole zero-field mobility. <math>(cm^{2}eV^{-1}s^{-1})</math> | ||
* βh : hole beta. <math>(eV^{-1/2})</math> | * βh : hole beta. <math>(eV^{-1/2})</math> | ||
* <math> | * <math>v_{n,sat}</math> saturate electron velocity (cm/s) | ||
* <math> | * <math>v_{p,sat}</math> saturate hole velocity (cm/s) | ||
<math>\mu_{n,temp}=\mu_0 exp(\beta\sqrt{E})</math>, <math>\mu_{p,temp}=\mu_0 exp(\beta\sqrt{E})</math> | <math>\mu_{n,temp}=\mu_0 exp(\beta\sqrt{E})</math>, <math>\mu_{p,temp}=\mu_0 exp(\beta\sqrt{E})</math> | ||
<math> \ | |||
If <math> \mu_{n,temp} \times E > v_{n,sat}, then \mu_n = \frac{v_{n,sat}}{E} </math> | |||
If <math> \mu_{p,temp} \times E > v_{p,sat}, then \mu_p = \frac{v_{p,sat}}{E} </math> | |||
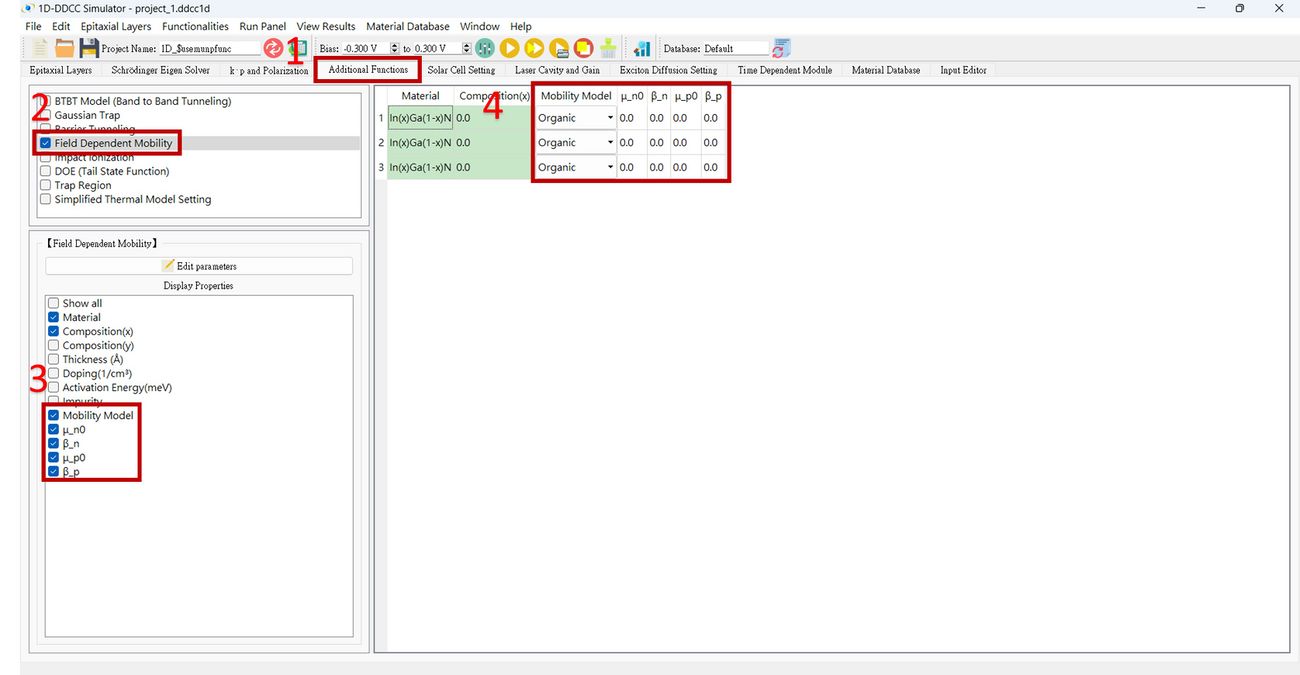
<big>'''The $usemunpfunc setting for 1D-DDCC in GUI interface '''</big> <br> | |||
The parameters are modified in step 4.<br> | |||
[[檔案:1d_$usemunpfunc_fig1.jpg|1300px]]<br> | |||
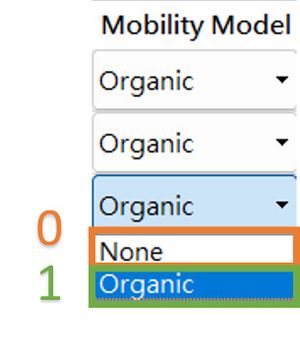
[[檔案:1d_$usemunpfunc_fig2.jpg|300px]]<br> | |||
於 2025年1月6日 (一) 11:36 的最新修訂
Function for organic material. We usually assume the carrier mobility is depend on electrical field and follow Poole-Frenkel field dependent mobility equation.
Mobility follow this equation
Where
- is the zero-field mobility
- is the factor of mobility increasing
- is the electric field.
Format
$usemunpfunc 1 μe βe μh βh
Parameter Explanation
,
- μe : electron zero-field mobility.
- βe : electron beta.
- μh : hole zero-field mobility.
- βh : hole beta.
$usemunpfunc 11 μe βe μh βh
Parameter Explanation
- μe : electron zero-field mobility.
- βe : electron beta.
- μh : hole zero-field mobility.
- βh : hole beta.
- saturate electron velocity (cm/s)
- saturate hole velocity (cm/s)
,
If If
The $usemunpfunc setting for 1D-DDCC in GUI interface