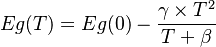$ifapplyEgofT

Since the DDCC has the capability of solving the Poisson, drift-diffusion, and thermal solver self-consistently. It will need to consider the possibility of bandgap narrowing with temperature. Therefore, we can apply the temperature-dependent coefficients for the material's bandgap. Usually, the temperature-dependent bandgap can be expressed as:

 $Eg(T) = Eg(0) - \frac{\gamma \times T^{2} }{ T + \beta}$

Therefore, to enable the temperature-dependent Eg in the simulation, we need to add
.

$ifapplyEgofT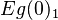
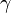
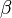
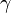
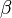
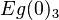
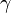
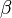
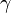
$Eg(0)_{1}$  $\gamma$  $\beta$
$Eg(0)_{2}$  $\gamma$  $\beta$
$Eg(0)_{3}$  $\gamma$  $\beta$
$Eg(0)_{4}$  $\gamma$  $\beta$
...
...
to layer N

If some material's coefficient cannot be found, please make 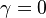$\gamma = 0$. So the program will keep the bandgap of this region as constant.
Note that

Eg(0) is the Eg at 0K, not 300K. So if the parameters source is not the same, 
 $Eg(300) = Eg(0) - \frac{\gamma \times 300^{2} }{ 300 + \beta}$ may not be the same as the Eg in the $parameters. Please be careful to use this command. 

For advanced users who use libmodpar.f90. This function may have problem if the bandgap is changed in libmodpar.f90

The related commands are: $ifapplytauofT, $ifapplymuofT, $ifapplyEgofT, $ifTversusJ